Center of Gravity

Table of contents

Center of mass - Analytical
Center of mass - From CAD
Center of mass by measuring
Video lecture (swedish)

Center of mass - Analytical

To determine the analytical location of the center of gravity of the above body we could compute the moments of all small bodies and compute the resulting moment by adding all moments. After which we can divide by the total weight to get the moment arm, which is the vector form of the center of mass.

\bm M = \sum \bm M_i = \sum \bm r_i \times \bm W_i

dividing by the total weight, $W$ , we get the center of mass

\bar{\bm r} = \dfrac{\bm M}{\bm W} = \frac{\sum \bm r_i \times \bm W_i}{\sum \bm W_i}

In most traditional books this is written out on component form, i.e.,

\bar x = \frac{\sum x_i W_i}{\sum W_i}, \quad \bar y = \frac{\sum y_i W_i}{\sum W_i}, \quad \bar z = \frac{\sum z_i W_i}{\sum W_i}

We said center of mass, but the above is expressed as a weight, well we can substitute $W = mg$ where $g$ is a constant and get

\bar{\bm r} = \frac{\sum \bm r_i m_i}{\sum m_i}

If the density, $\rho$ , of a body can be assumed to be constant we can express the center of mass purely as a geometrical property

\bar{\bm r} = \frac{\sum \bm r_i V_i}{\sum V_i}

here $V$ denotes volume but can also be area or line length.

For general bodies we need to add up all small weight, masses, or spatial elements, forming an integral

\bar{\bm r} = \frac{\int \bm r dV}{\int dV} = \frac{\int \bm r dV}{V}

Center of mass - From CAD

In practice, we use a CAD system to compute the center of mass, since the analytical approach is tedious even for slightly complex object and practically impossible for anything moderately complex.

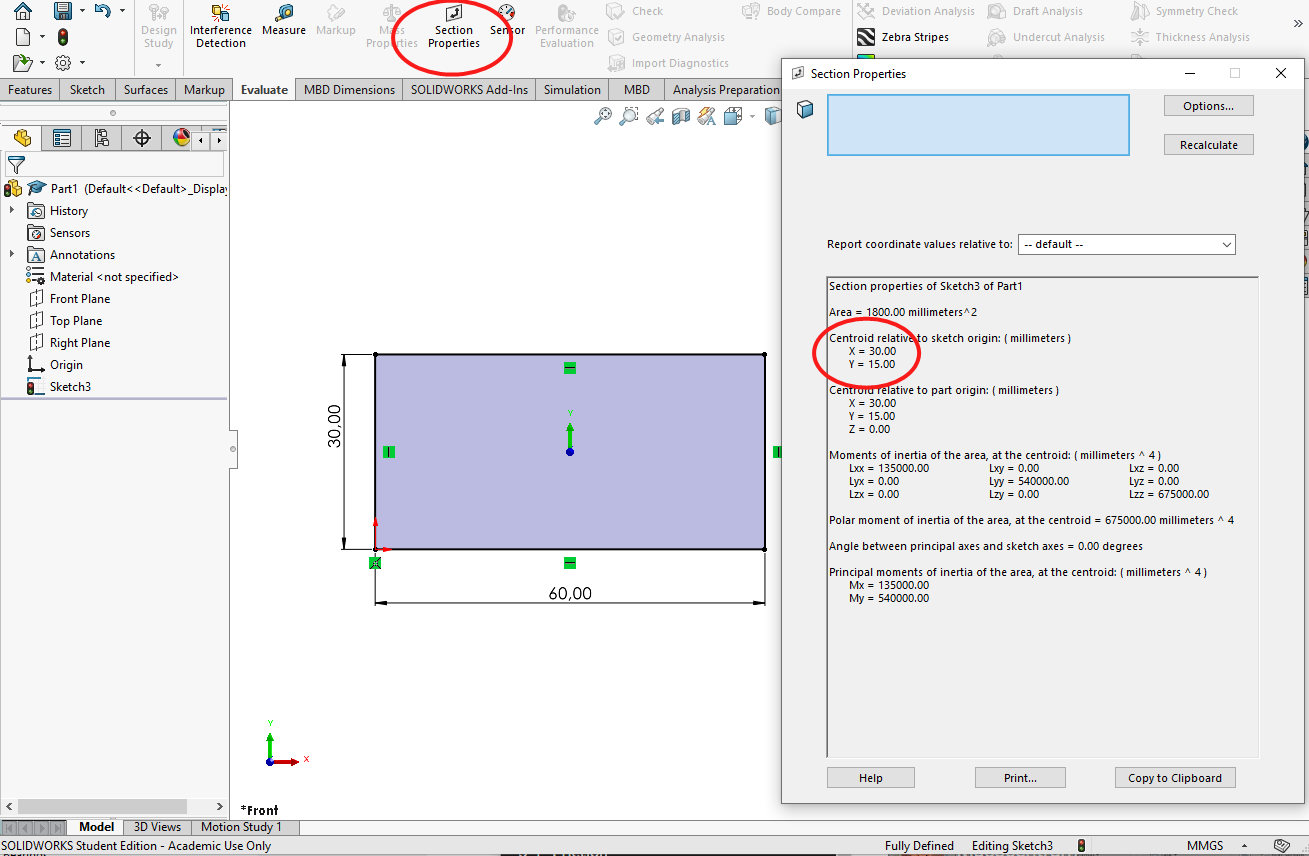
For this simple 2D shape the origin is in the lower left corner and thus the center of mass is at $x=30$ mm and $y=15$ mm. We can determine this using SolidWorks, by creating the sketch as a closed shape and going to Evaluate and Section Properties.

For three dimensional objects such as this below

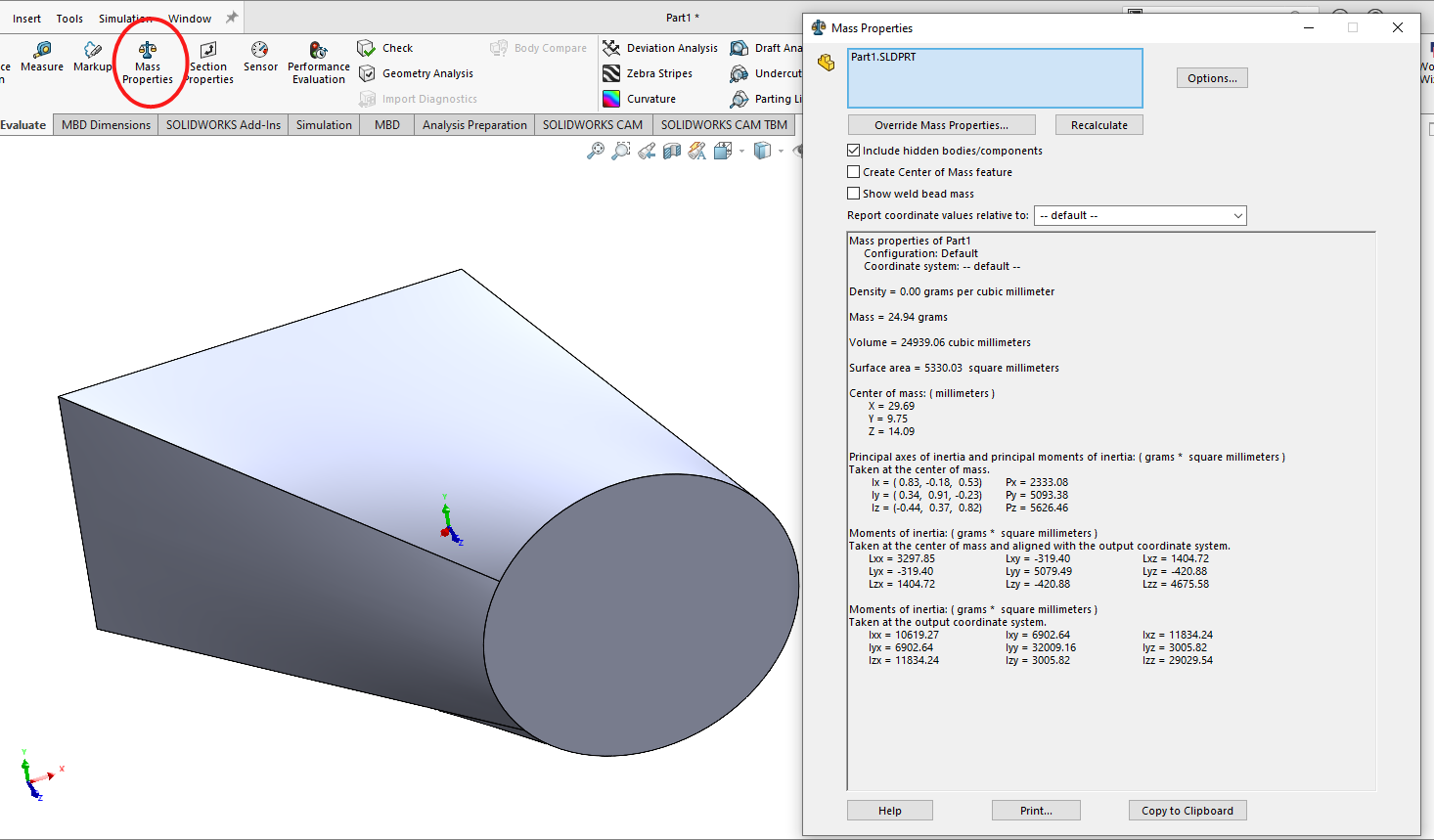
we go to Evaluate and Mass Properties where we get all geometrical properties, we shall return to this tool in later chapters.

If we need to determine the center of a infinitely thin object we can draw it as a line and do a thin offset using the Offset Entities tool.

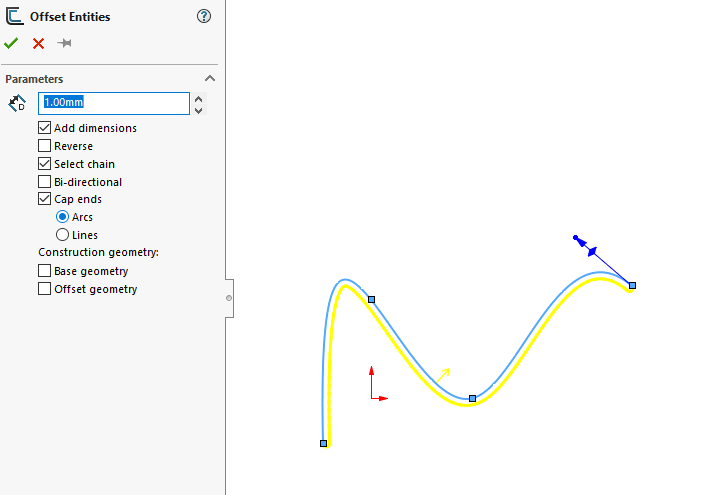
after which we can use the Section Properties tool to get the desired information.

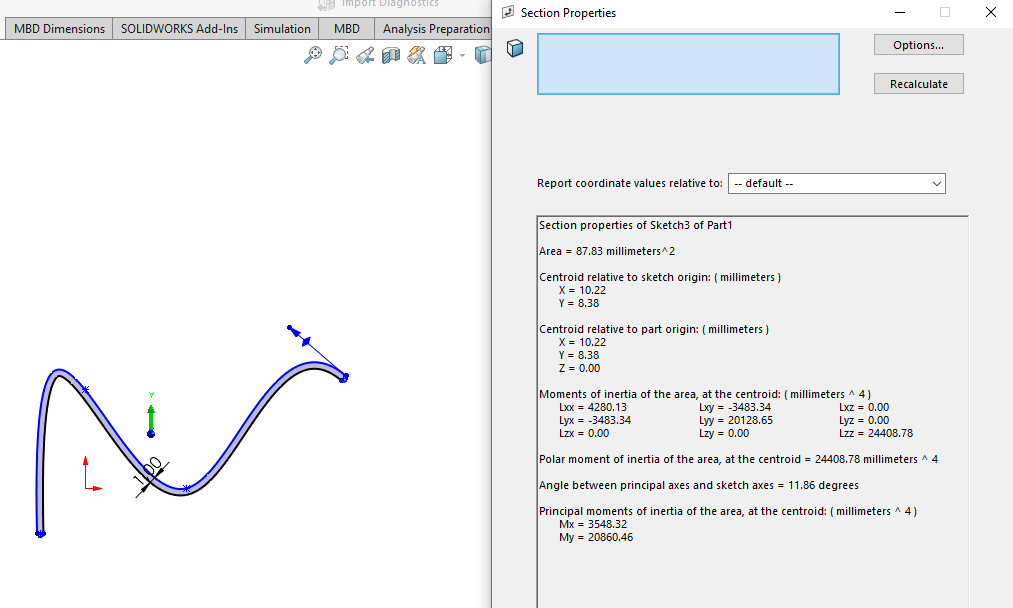
Thus we can keep the discussion of center of mass to a minimum and skip computing countless examples of trivial cases for the sake of filling a course with material.

Applied Mechanics

Center of Gravity

Center of mass - Analytical

Center of mass - From CAD

Center of mass by measuring

Video lecture (swedish)