MaterialProperties

Table of contents

Young's Modulus and Hooke's law in 1D
Transversal strain

Young's Modulus and Hooke's law in 1D

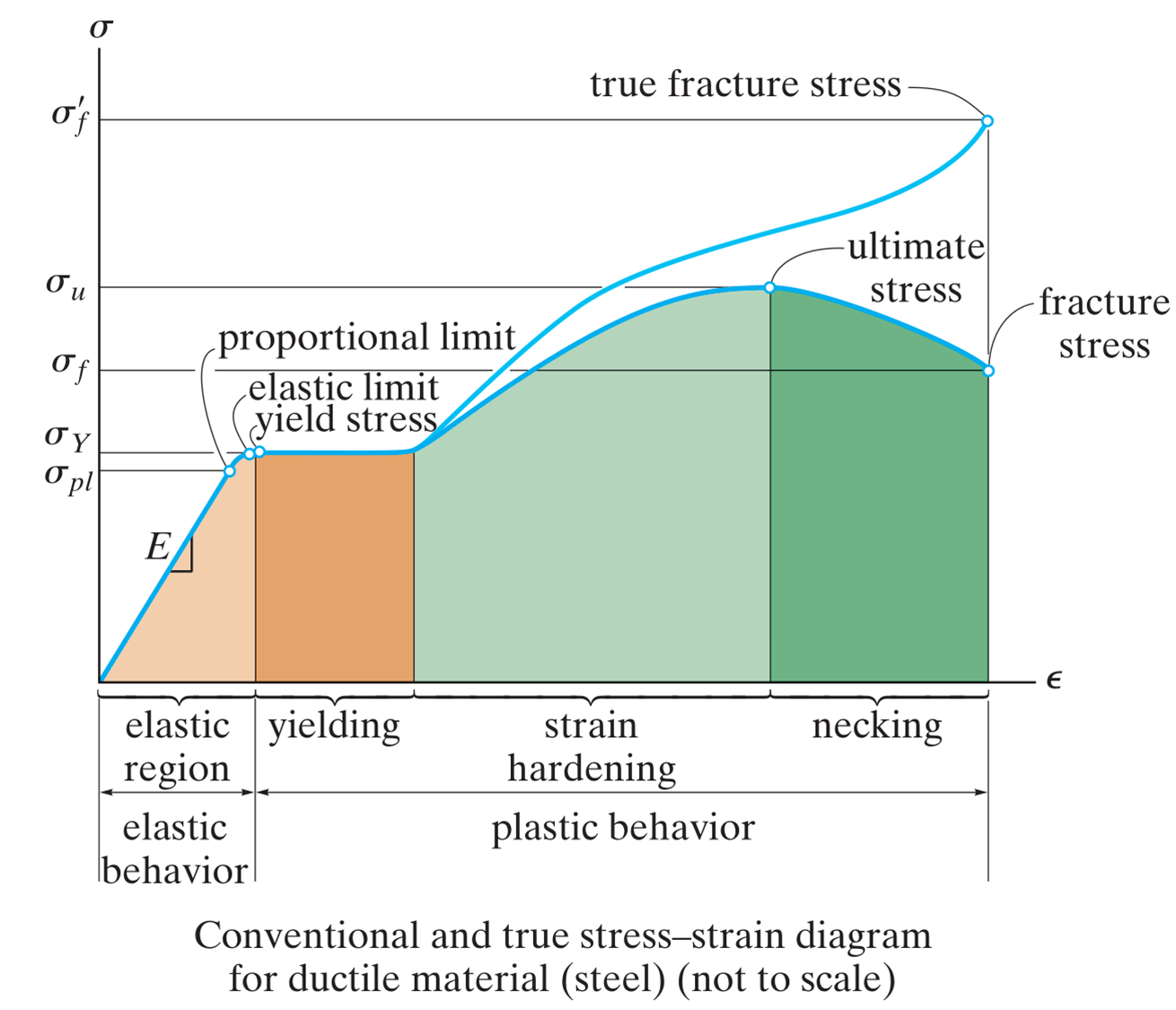
There are many material properties, constitutive relations, that relate strain to stress. The simplest of these is Hooke's law, which gives the linear relation

\sigma =E\varepsilon

where $E$ denotes the Young's modulus, or modulus of elasticity. Hooke's law is only valid in the elastic region of a material. Note that not all materials have a well-defined elastic region if at all. The elastic region is defined by the fact that the deformation increases linearly with the external force and that the deformation returns to zero once the external load is removed.

The Young's modulus is given experimentally using e.g., a tensile test to generate a stress - strain curve from which the Young's modulus can be obtained. The definition is:

E:=\dfrac{\Delta \sigma }{\Delta \varepsilon }=\dfrac{F/A}{\Delta L/L_0 }=\dfrac{F\;L_0 }{A\Delta L}

which is valid when $\Delta L << L$ .

Young's modulus can be seen as a stiffness of the material.

Typical values are $E_{\textrm{steel} } =210,000\textrm{MPa}$ , $E_{\textrm{Aluminium} } =68,000\textrm{MPa}$ , $E_{\textrm{Titanium} } =115,000\textrm{MPa}$ but these vary due to e.g., composition, temperature and strain rate just to mention a few. Young's modulus is not evenly distributed in material, especially casted or 3D printed materials are not homogenous.

If the material has different stiffness properties in different direction (x,y, z) then it is said to be an-isotropic instead of iso-tropic.

See more on the topic at the Efficient Engineer channel.

Transversal strain

\nu =\dfrac{-\varepsilon_{\textrm{lat} } }{\varepsilon_{\textrm{long} } }=\dfrac{-\varepsilon_y }{\varepsilon_x }

\varepsilon_y =-\nu \varepsilon_x

See more on the topic:

Applied Mechanics

Young's Modulus and Hooke's law in 1D

Transversal strain