Moments

Download this page as a Matlab LiveScript

Table of contents

Moment or Torque
Example 1 - 2D Trivial case
Example 2 - 2D general
Example 3 - 3D case
Example 4 - General projection

Moment or Torque

A moment, also known as the torque can be described as a "force to generate a rotation", as it generates an angular acceleration if not in ballance.

A moment has the unit Newton-meter [Nm], it is a vector, and appears around a point as the product of a moment arm (hävarm), $d$ , and an applied force, $F$ , perpendicular to the moment arm, see the figures below.

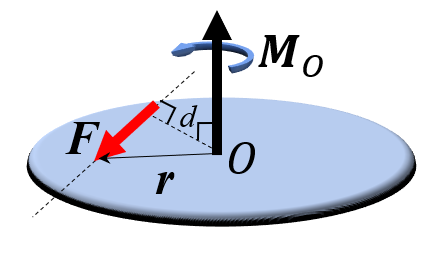
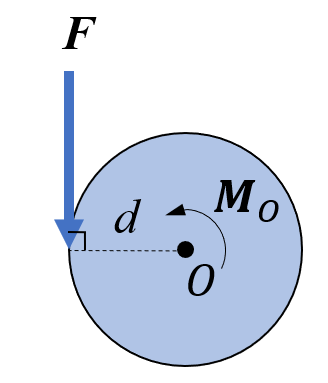
{\mathit{\mathbf{M} } }_O =\mathit{\mathbf{r} }\times \mathit{\mathbf{F} }

and the scalar counterpart

M=F\;d

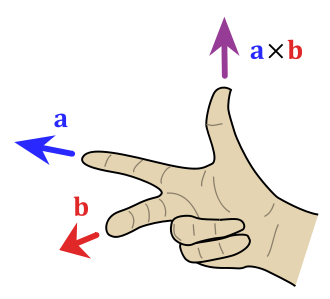
The moment vector is defined as the vector $\mathit{\mathbf{M} }$ that is perpendicular to the plan that is spanned by the position vector, $\mathit{\mathbf{r} }$ and the force vector $\mathit{\mathbf{F} }$ . The direction of the moment vector is given by the right-hand rule.

$\mathit{\mathbf{r} }$ is a position vector from the point about which the moment is being calculated to the line along which $\mathit{\mathbf{F} }$ is acting (action line).

In Matlab we compute the cross product by

syms F_x F_y F_z 
syms r_x r_y r_z
F = [F_x F_y F_z].';
r = [r_x r_y r_z].';
M = cross(r,F)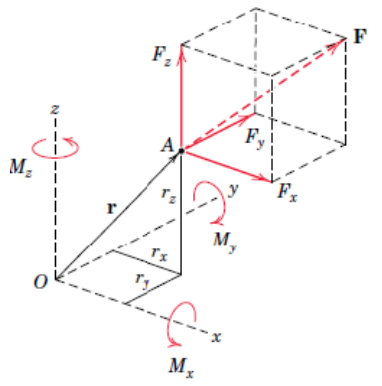

\left(\begin{array}{c} F_z \,r_y -F_y \,r_z \\ F_x \,r_z -F_z \,r_x \\ F_y \,r_x -F_x \,r_y \end{array}\right)

{\mathit{\mathbf{M} } }_O =\left\lbrack \begin{array}{c} M_x \\ M_y \\ M_z \end{array}\right\rbrack =\left\lbrack \begin{array}{c} F_z \,r_y -F_y \,r_z \\ F_x \,r_z -F_z \,r_x \\ F_y \,r_x -F_x \,r_y \end{array}\right\rbrack =\left\lbrack \begin{array}{c} F_z \,r_y -F_y \,r_z \\ -\left(F_z \,r_x -F_x \,r_z \right)\\ F_y \,r_x -F_x \,r_y \end{array}\right\rbrack =\mathit{\mathbf{r} }\times \mathit{\mathbf{F} }

\mathit{\mathbf{M} }=\mathit{\mathbf{r} }\times \mathit{\mathbf{F} }=-\mathit{\mathbf{F} }\times \mathit{\mathbf{r} }

\mathit{\mathbf{M} }\bot \mathit{\mathbf{r} }\;\textrm{and}\;\mathit{\mathbf{M} }\bot \mathit{\mathbf{F} }

1: Trivial examples of how the cross product works, showcasing the independency on the point of application along the line of application.

Example 1 - 2D Trivial case

clear
r = [3,0,0];
F = 10*[0,1,0];
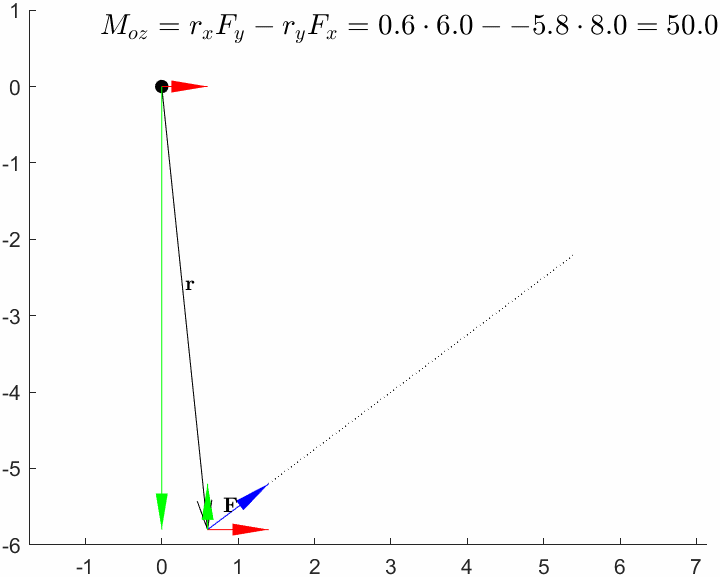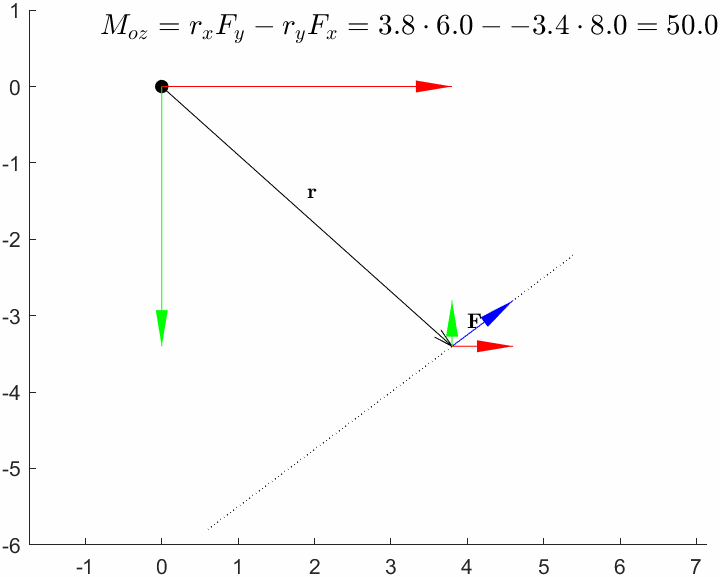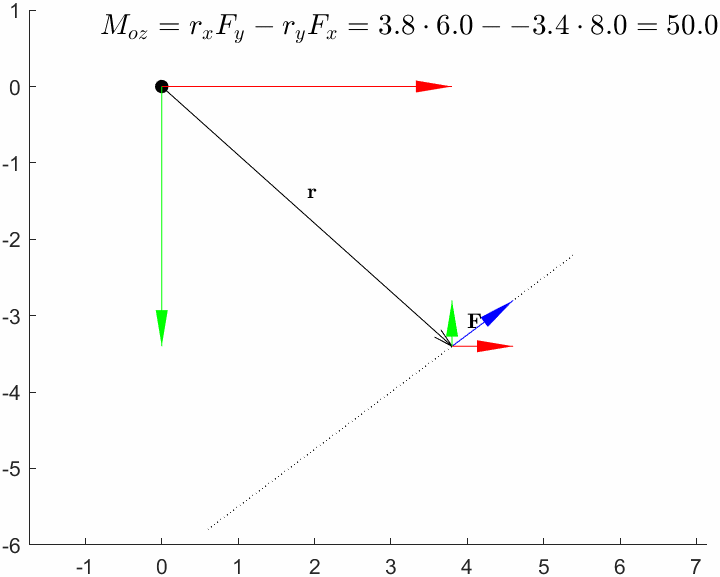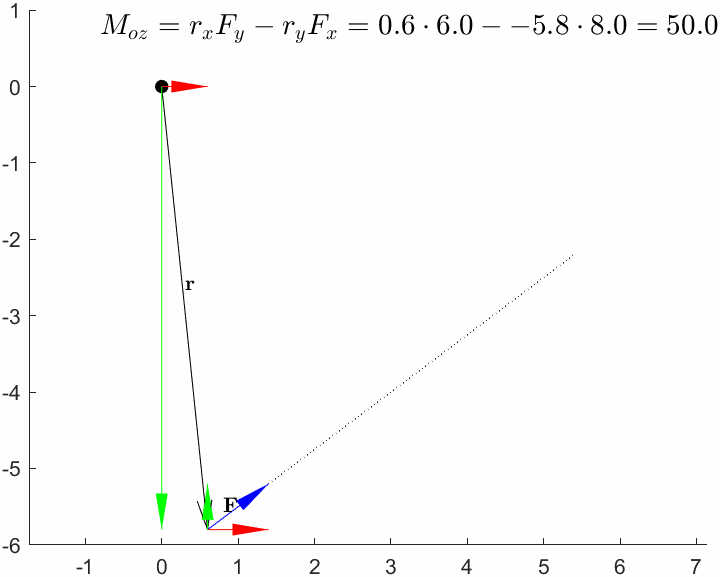
Mz = 3*10

Mz = 30

M = cross(r,F)

M = 1x3    
     0     0    30

Note that the $y$ component in r can take any value, and the moment around $z$ will be the same, this is obvious since the $x$ distance does not change.

Example 2 - 2D general

eF = [4/5, 3/5, 0];
F = 10*eF;
OA = [3,-4,0];
Mz = 5*10

Mz = 50

M = cross(OA,F)

M = 1x3    
     0     0    50

t=2;
r = OA + [4/5,3/5,0]*t

r = 1x3    
     4.6    -2.8     0

M = cross(r,F)

M = 1x3    
     0     0    50

Here we can vary the parameter $t$ to set the point of application to any point along the line of application and the moment around the $z$ axis will be unaffected. In fact we can set the parameter $t$ to a symbolic variable and we can see that $t$ vanishes in the cross product.

syms t
r = OA + [4/5,3/5,0]*t
M = cross(r,F)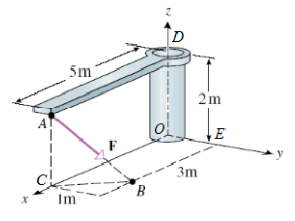

\bm r = \left(\begin{array}{ccc} \frac{4\,t}{5}+3 & \frac{3\,t}{5}-4 & 0 \end{array} \right)

\bm M = \left(\begin{array}{ccc} 0 & 0 & 50 \end{array}\right)

Example 3 - 3D case

Let $F=100\mathrm{N}$ in the line AB. Determine the moment O. Determine the moment around the z-axis.

\overrightarrow{\textrm{OA} } ={\left\lbrack 5,0,2\right\rbrack }^T

\overrightarrow{\textrm{OB} } ={\left\lbrack 3,1,0\right\rbrack }^T

\mathit{\mathbf{r} }=\overrightarrow{\textrm{OB} }

\mathit{\mathbf{F} }=F\;{\mathit{\mathbf{e} } }_{\textrm{AB} }

{\mathit{\mathbf{e} } }_{\textrm{AB} } =\dfrac{\overrightarrow{\textrm{AB} } }{|\overrightarrow{\textrm{AB} } |}

{\mathit{\mathbf{M} } }_O =\mathit{\mathbf{r} }\times \mathit{\mathbf{F} }

M_{\textrm{Oz} } =M_O \cdot {\mathit{\mathbf{e} } }_z

clear
OA = [5,0,2]';
OB = [3,1,0]';
AB = OB-OA;
eAB = AB/norm(AB)

eAB = 3x1    
   -0.6667
    0.3333
   -0.6667

F = 100*eAB

r = OB;

MO = cross(OA,F)

MO = cross(OB,F)

MOz = dot(MO,[0,0,1])

MOz = 166.6667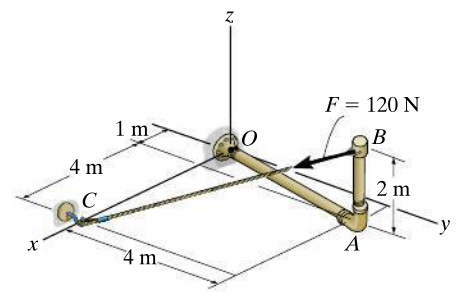

Example 4 - General projection

Compute the moment around the OA axis.

OA = [1,4,0].';
OB = [1,4,2].';
OC = [5,0,0].';
BC = OC-OB;
F = 120*BC/norm(BC)

MO = cross(OB,F)

MO = cross(OC,F)

eOA = OA/norm(OA)

M_{\textrm{OA} } ={\mathit{\mathbf{M} } }_O \cdot e_{\textrm{OA} } =\left|\dfrac{M_O \cdot \overrightarrow{\textrm{OA} } }{\overrightarrow{\textrm{OA} } \cdot \overrightarrow{\textrm{OA} } }\overrightarrow{\textrm{OA} } \right|

MOA = norm(dot(MO,OA)/dot(OA,OA)*OA)

MOA = 194.0285

MOA = dot(MO,eOA)

MOA = 194.0285