Applied Mechanics

Table of contents

Introduction to solid mechanics - stress

Watch the video by The Efficient Engineer.

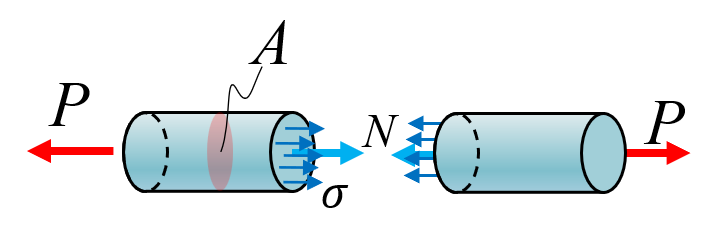
A bar is loaded along its axis with a force $P$. We can analyze the stress acting on the rod by cutting perpendicular to the rod and applying a free body diagram on one (or both sides).

From either side we get the force equilibrium

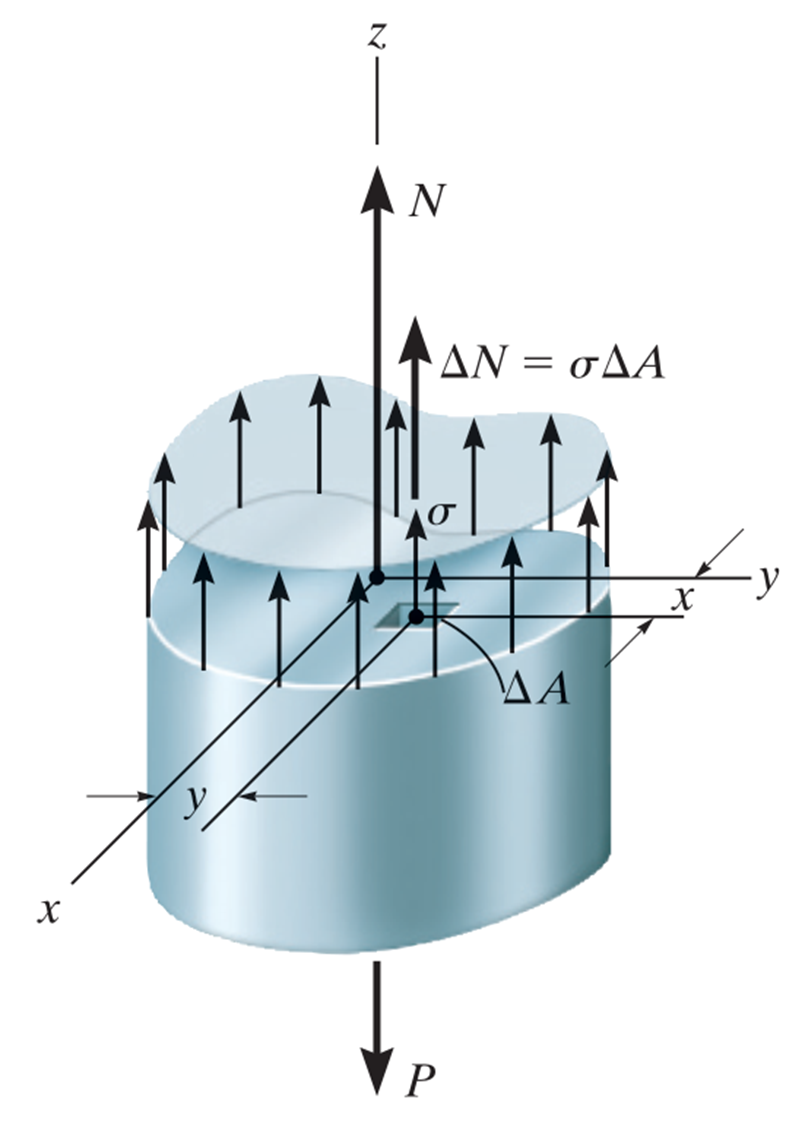
The normal force is always defined positively out from the surface. Doing the cut such that the normal force is parallel to the axis we can formulate the ballance of external and internal forces, where the internal forces is defined as the sum of infinitely many small forces, which can instead be represented as the product of the average normal stress and the cross-sectional area or more rigorously:

from which we get the definition of the normal stress

or on average

where $A$ is the cross sectional area of the rod in ${\textrm{mm} }^2$. Thus the unit of the stress is $N/{\textrm{mm} }^2$ or $\textrm{MPa}$ (mega Pascal).

To summarize, a cut and a free body diagram will give rise to two equations

Positive stress is defined as tension and negative as compression, these are known as tensile stress and compressive stress.

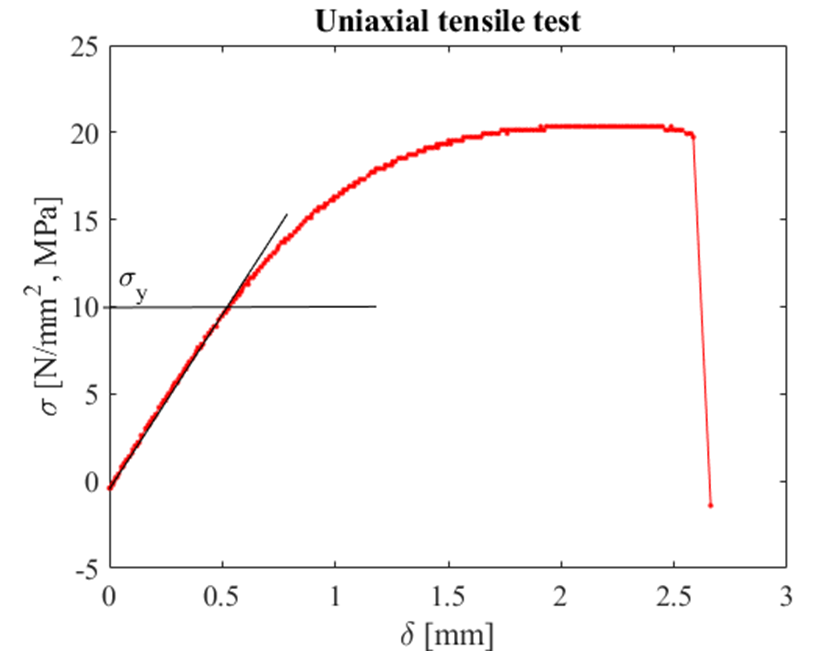
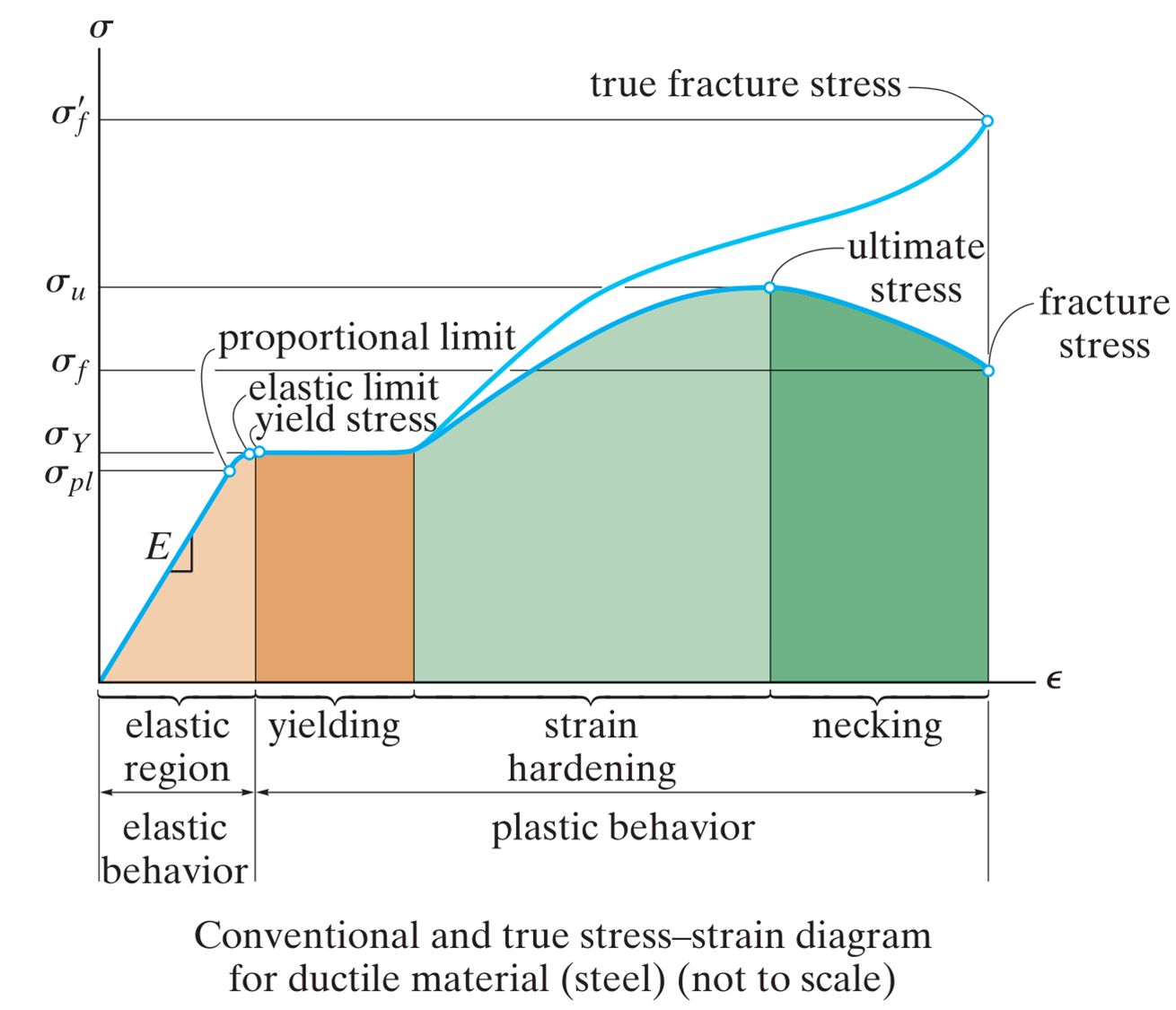
In stress analysis we are interested in the yield stress of a material, often we get this stress limit from a tensile test of a specimen. The yield stress is defined as the limit just before the material undergoes plastic deformation. The yield stress is the upper limit of the elastic region, which is the region in which the material will spring back to its undeformed shape when a load is removed.

See more information on the stress - strain diagram here.

Example 1 - dimensioning

The maximum allowable stress for a material is 150MPa and a rod needs to carry 8kN of tensile load, what is the minimum diameter of the rod in whole mm?

Solution

We have

Now, if we were to round to the nearest whole mm, we'd get $d=8\ldotp 0\textrm{mm}$ and $\sigma =\frac{8000}{\pi \cdot {\left(8\ldotp 0/2\right)}^2 }\approx 159\textrm{MPa}$ which is more than the allowable stress, so we need to round up to the nearest mm instead! With $d=9\ldotp 0\;\textrm{mm}$ we get

and the factor of safety then becomes

which means that the design with a diameter of 9mm can carry around 19% more load before its maximum allowable stress is

Example 2 - Stress computation

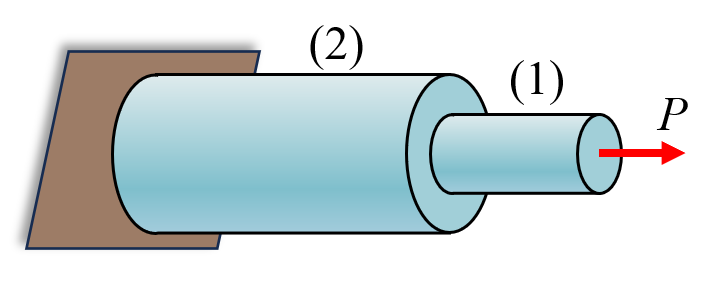
A bar is made up of two cross sections as shown in the figure. Cross section 1 has an area $A_1 =10{\;\textrm{mm} }^2$ and cross section 2 has an area $A_2 =2A_1 \;{\textrm{mm} }^2$. The applied tension force is $P=10$kN. Determine the stress in both parts. Which part has the highest stress?

Solution

Two cuts and Free body diagrams

Cut 1 at (1):

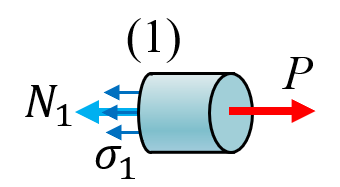
and cut 2 at (2):

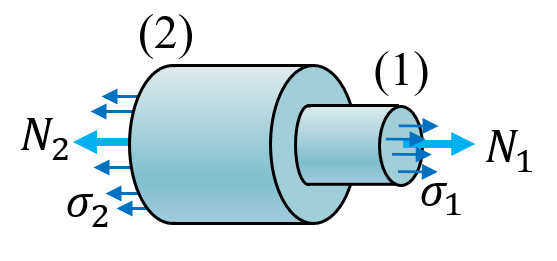
clear
syms N_1 N_2 A_1 A_2 P sigma_1 sigma_2

ekv = [N_1-P==0; N_2-P==0 % Equilibrium
       sigma_1 == N_1/A_1; sigma_2 == N_2/A_2
       P == 10e3
       A_1 == 10^2; A_2 == 2*A_1]

[N_1, N_2, sigma_1, sigma_2, P, A_1, A_2] = solve(ekv, [N_1, N_2, sigma_1, sigma_2, P, A_1, A_2])

Here we see another way of using solve, we simply input all the information as a list of equations and ask to solve for the same amount of variables as the number of equations.

Conclusion: $\sigma_1 =100$ MPa and $\sigma_2 =50$ MPa. The stress is higher in the narrow region, as expected, since there is less material to balance the external force.

Example 3

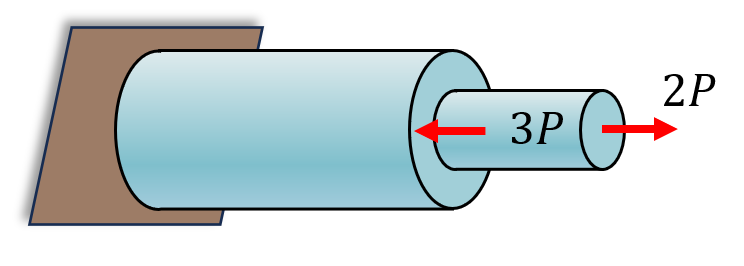
Same as last example, but with more external forces.

Solution: Here we will have two cuts and three bodies according to the free body diagram

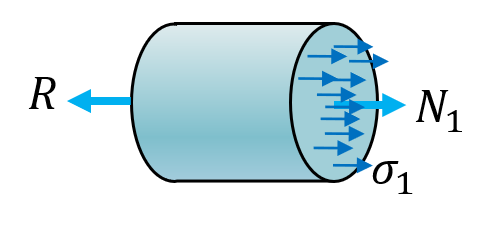
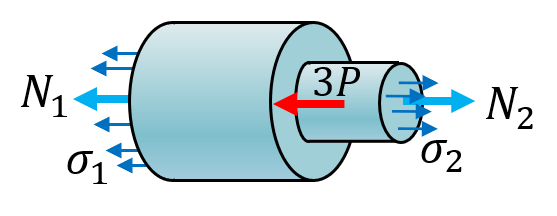
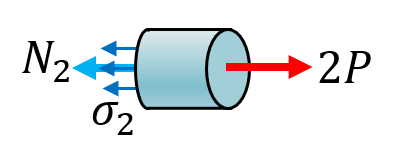
From these we get the equations

clear
syms N_1 N_2 A_1 A_2 P sigma_1 sigma_2 R

ekv = [N_1-R==0; N_2-3*P-N_1==0; 2*P-N_2==0
       sigma_1==N_1/A_1; sigma_2==N_2/A_2]

[N_1, N_2, R, sigma_1, sigma_2] = solve(ekv, [N_1, N_2, R, sigma_1, sigma_2])

Here we see that we get compression stress in 1 since $\sigma_1 =-\frac{P}{A_1 }$, the largest stress is in 2 though since the magnitude of that tensile stress is $2P/A_2$.

Example 4 - Sausage stress - Cylinder stress

It is BBQ season, and always a time for structural analysis. In this case we wonder why the Bratwurst always tends to crack along the longest axis and not along the width.

Solution: We model the sausage as a cylinder where the length is much larger than the radius. We will use a cylindrical coordinate system with $\varphi$ defining the tangential direction, $r$ the radial direction and $z$ the axial direction.

Let $L$ denote the length, let $R << L$ denote the radius and $t << R$ the thickness. Furthermore, let $p$ denote the inner pressure $\left\lbrack N/{\textrm{mm} }^2 \right\rbrack$. Now, let's slice the sausage along its length and width.

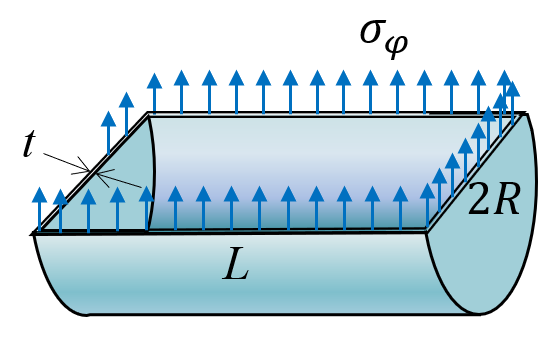
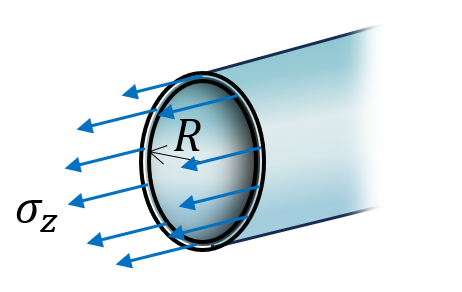
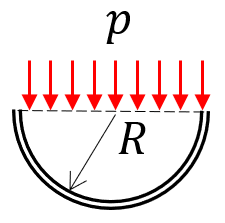
Now we formulate the equilibrium equations

since $Rt << hL$ we can neglect the second term in the first equation.

clear
syms sigma_varphi t L R p sigma_z
ekv = [sigma_varphi*2*t*L - p*2*R*L == 0
       sigma_z*2*pi*R*t - p*pi*R^2 == 0]

[sigma_varphi, sigma_z] = solve(ekv,[sigma_varphi, sigma_z])

We note that $\sigma_{\varphi } =2\sigma_z$, meaning if the Bratwurst cracks, it will crack along the axial direction.

Example 5

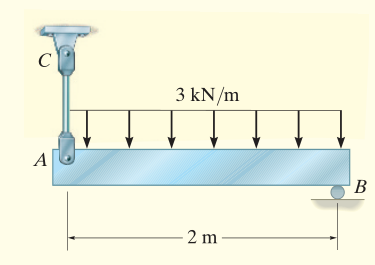
The 400 kg uniform bar AB is supported by a steel rod AC and roller at B. It supports a distributed load of $3\textrm{kN}/\mathrm{m}$. Determine the required diameter of the rod AC. The yield stress of the material is 345 MPa and the factor of safety is 1.2.

Solution:

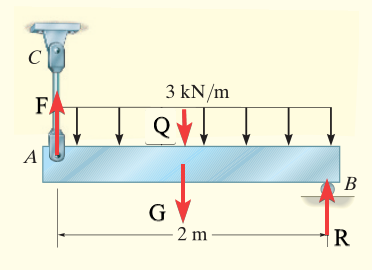
The distributed load can be replaced by a point load acting from the center of the distributed load.

Then we have simply

clear
syms F R
Q = 6e3;
G = 400*9.82;
ekv = [F - Q - G + R == 0
       Q*1 + G*1 - F*2 == 0]

[F,R] = solve(ekv,[F,R])

sigma = 345/1.2

sigma = 287.5000

syms d positive
d = solve(sigma == F/(pi*(d/2)^2));
double(d)

ans = 4.6887

Answer: The diameter should be at least 5mm