Table of contents
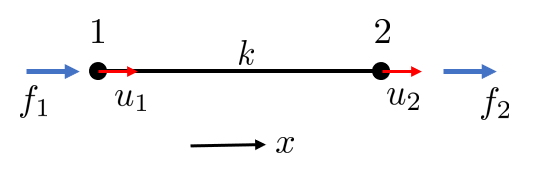
One dimensional rod with two displacements and two forces.
Recall a spring force: , now we apply this on our case
where . With and we can write
or on matrix form
or
where is known as the element stiffness matrix.
Now, consider some arbitrary rod in a two dimensional setting.
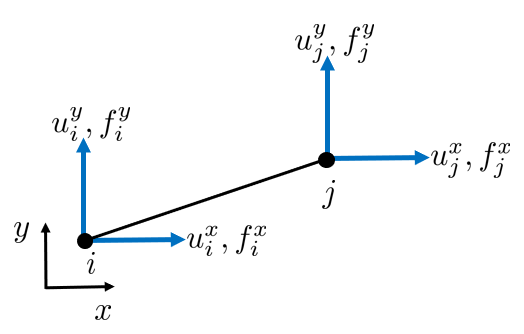
Each node can be translated in the x- and y-direction and each node can carry loads in x- and y-directions.
We shall derive the element stiffness matrix for this rod, but it is easier to first derive it in local coordinates and then transform it into the global coordinates.

Each rod has a local coordinate system and and local node numbers and . The local coordinate system is rotated compared to the global coordinate system, and the angle is denoted by . In the local coordinates we have
We have zero force normal to the rod since the rod only can carry axial forces. The above relation can be written on matrix form
or
known as the local element stiffness matrix.
We need a way to transform to and . In other words, we need a relation between and and

which on matrix form is
or
where is known as the transformation matrix, and we recognize the rotation matrix within. The transformation matrix has interesting properties: and .
Using the transformation matrix we can transform local quantities to global
or
where is known as the element stiffness matrix.
One could determine the angle . But there is a cheaper way. Let define the rod vector such that
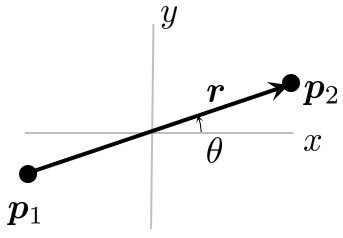
then the normalized vector
such that we get
and
We note that the element stiffness matrix is symmetric.
Does it matter how the rod vector is defined? The vector can be defined either by or and we get two situations.
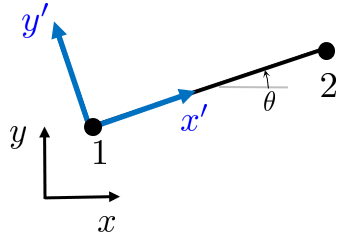
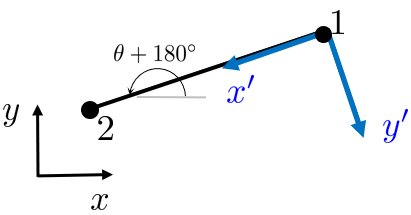
It turns out (which is easily verifiable) that is independent of the how the rod vector (or angle ) is defined, i.e., both alternatives yield the same result.
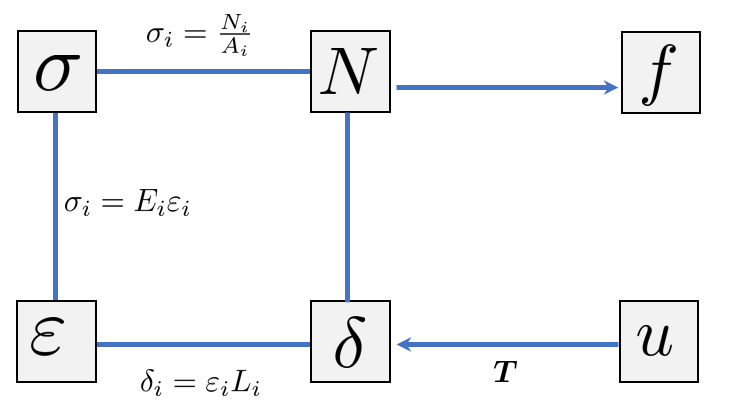
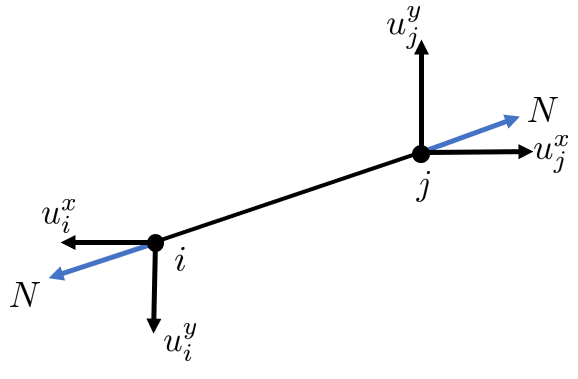
The deformation of the rod is given by
where is called the transformation vector.
We have the rod element rod force
and the element load vector (or reaction forces)
The element strain is obtained by
and the stress by
note that the length of the element can be easily computed by
Let us analyze a structure as an example and look at the implementation details in Matlab.
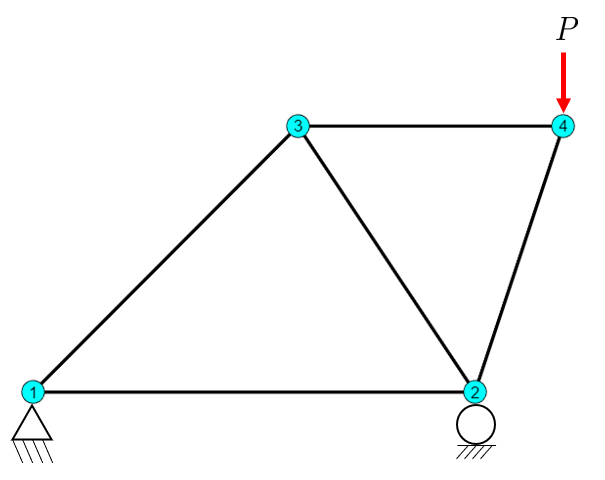
The structure is loaded by a force with the topology given by
P = [0 0
5 0
3 3
6 3]*100; % mm
edges = [1 2
1 3
2 3
2 4
3 4];Problem statement:
Given the structure above, determine all displacements, member forces, deformations, strains and stresses as well as reaction forces in the supports.
Solution
The coordinates are given by the variables P and the edges define the node connectivity.
The order of the columns in nodes is not important.
Using the topological data from above, we can visualize the truss structure in Matlab as follows:
figure
hold on
patch('Faces',edges,'Vertices',P,'LineWidth',2)
plot(P(:,1),P(:,2),'ok','MarkerFaceColor','c','MarkerSize',14)
nnod = size(P,1);
text(P(:,1)-0.05,P(:,2),cellstr(num2str([1:nnod]')))
axis equal
axis off
for i=1:5
inod = edges(i,:);
xm = mean(P(inod,1));
ym = mean(P(inod,2));
text(xm,ym,num2str(i),'backgroundColor','y')
end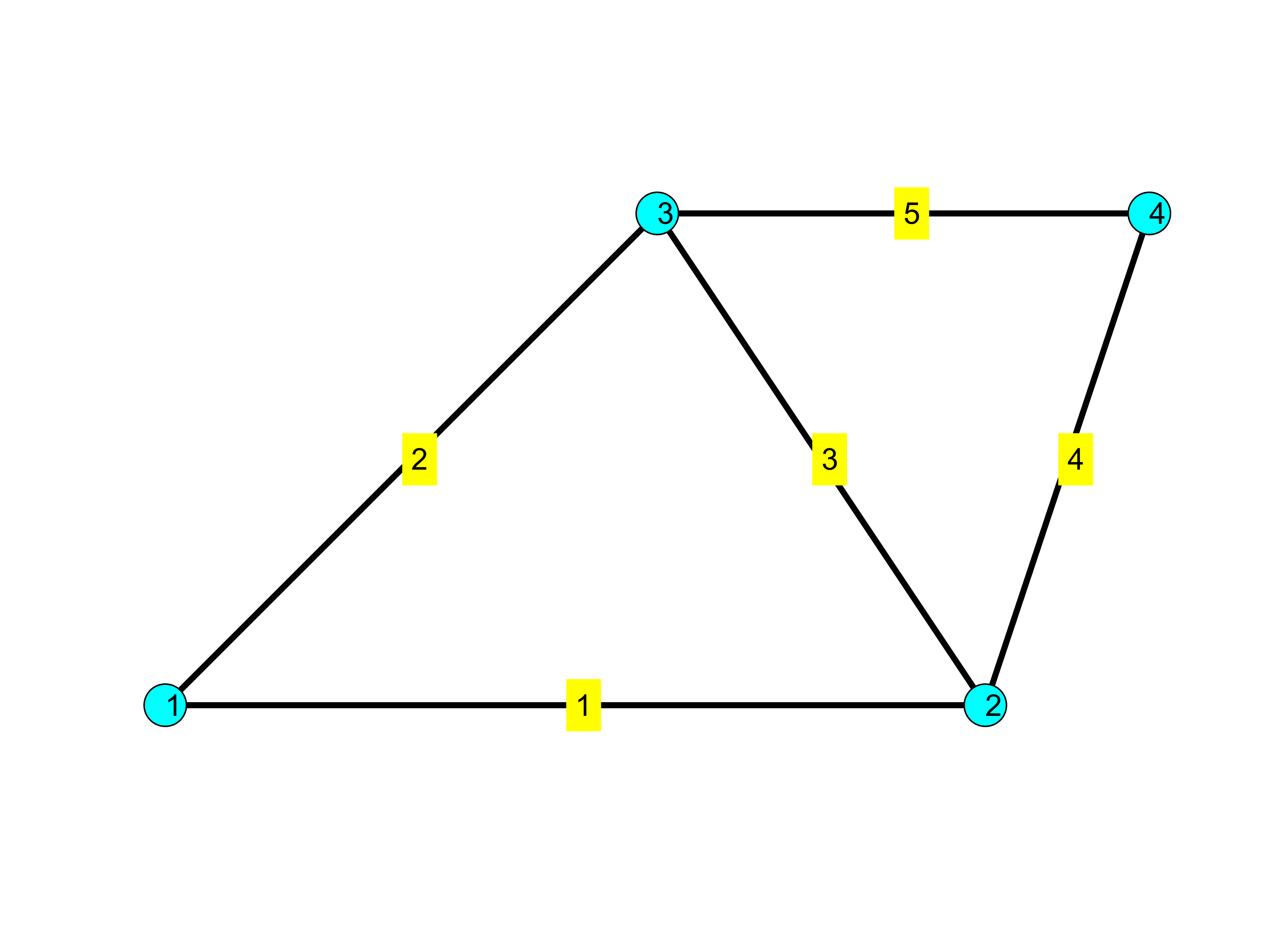
The total number of degrees of freedom (or equations), is given by
where is the number of nodes and is the number of local degrees of freedom per node.
The global displacement field and load field are given by
With the resulting linear system taking the form of
The unknown displacements are computed by establishing the global stiffness matrix (system matrix) . Creating the linear system (28) and solving for . This is done by the following steps:
Initialize the stiffness matrix, i.e., set it to zero, .
Loop over all elements, and for each element:
Compute the element stiffness matrix,
Add the element stiffness matrix into the global stiffness matrix
Add the element load vector to the global load vector
Apply boundary conditions
Solve the linear system
We begin with some preliminaries and initialize the global system matrix and vectors using the number of degrees of freedom.
nele = 5nnod = 4dofs = 8S = zeros(dofs, dofs);
f = zeros(dofs,1);
u = f;
Sprim = [1 0 -1 0
0 0 0 0
-1 0 1 0
0 0 0 0];
Ltot = 0; %Total length of the structure.
E = 210000*ones(nele,1); % Young's modulus
A = 4*6*ones(nele,1); % Cross sectional areaElement 1
We begin by computing which global degrees of freedom correspond to our first element.
inod = 1x2
1 2The node numbers correspond to degrees of freedom, for our problem we have two, i.e., and translation. The data structure of ieqs is the same as for the displacements and loads above.
ieqs = 1x4
1 0 3 0ieqs = 1x4
1 2 3 4Computing the element stiffness matrix
p1 = 1x2
0 0p2 = 1x2
500 0r = 1x2
500 0L = 500Ltot = 500er = 1x2
1 0LT = 4x4
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1k = 10080Se = 4x4
10080 0 -10080 0
0 0 0 0
-10080 0 10080 0
0 0 0 0Assembly process
The element stiffness matrix needs to be added to the global stiffness matrix . We need to ensure that the correct components from the element matrix are mapped to the corresponding components of the global stiffness matrix. This is done using the previously computed list of degrees of freedom, stored in the variable ieqs. We append (add) the stiffness contributions using
S = 8x8
10080 0 -10080 0 0 0 0 0
0 0 0 0 0 0 0 0
-10080 0 10080 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0This is the simplest form of assembly in code. It is easy to read and understand. It is however not very efficient for very large problems with hundreds of thousands of elements. So there exists other methods of dealing with this. But that is a topic for a course in high performance computing.
The rest of the elements are dealt with in an automated manner by executing the above lines of code for each element number, iel. This is done using the for loop:
iel = 2
L = 424.2641
Ltot = 924.2641
er = 1x2
0.7071 0.7071
k = 1.1879e+04
Se = 4x4
1.0e+03 *
5.9397 5.9397 -5.9397 -5.9397
5.9397 5.9397 -5.9397 -5.9397
-5.9397 -5.9397 5.9397 5.9397
-5.9397 -5.9397 5.9397 5.9397
S = 8x8
1.0e+04 *
1.6020 0.5940 -1.0080 0 -0.5940 -0.5940 0 0
0.5940 0.5940 0 0 -0.5940 -0.5940 0 0
-1.0080 0 1.0080 0 0 0 0 0
0 0 0 0 0 0 0 0
-0.5940 -0.5940 0 0 0.5940 0.5940 0 0
-0.5940 -0.5940 0 0 0.5940 0.5940 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
iel = 3
L = 360.5551
Ltot = 1.2848e+03
er = 1x2
-0.5547 0.8321
k = 1.3978e+04
Se = 4x4
1.0e+03 *
4.3011 -6.4516 -4.3011 6.4516
-6.4516 9.6774 6.4516 -9.6774
-4.3011 6.4516 4.3011 -6.4516
6.4516 -9.6774 -6.4516 9.6774
S = 8x8
1.0e+04 *
1.6020 0.5940 -1.0080 0 -0.5940 -0.5940 0 0
0.5940 0.5940 0 0 -0.5940 -0.5940 0 0
-1.0080 0 1.4381 -0.6452 -0.4301 0.6452 0 0
0 0 -0.6452 0.9677 0.6452 -0.9677 0 0
-0.5940 -0.5940 -0.4301 0.6452 1.0241 -0.0512 0 0
-0.5940 -0.5940 0.6452 -0.9677 -0.0512 1.5617 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
iel = 4
L = 316.2278
Ltot = 1.6010e+03
er = 1x2
0.3162 0.9487
k = 1.5938e+04
Se = 4x4
1.0e+04 *
0.1594 0.4781 -0.1594 -0.4781
0.4781 1.4344 -0.4781 -1.4344
-0.1594 -0.4781 0.1594 0.4781
-0.4781 -1.4344 0.4781 1.4344
S = 8x8
1.0e+04 *
1.6020 0.5940 -1.0080 0 -0.5940 -0.5940 0 0
0.5940 0.5940 0 0 -0.5940 -0.5940 0 0
-1.0080 0 1.5975 -0.1670 -0.4301 0.6452 -0.1594 -0.4781
0 0 -0.1670 2.4021 0.6452 -0.9677 -0.4781 -1.4344
-0.5940 -0.5940 -0.4301 0.6452 1.0241 -0.0512 0 0
-0.5940 -0.5940 0.6452 -0.9677 -0.0512 1.5617 0 0
0 0 -0.1594 -0.4781 0 0 0.1594 0.4781
0 0 -0.4781 -1.4344 0 0 0.4781 1.4344
iel = 5
L = 300
Ltot = 1.9010e+03
er = 1x2
1 0
k = 16800
Se = 4x4
16800 0 -16800 0
0 0 0 0
-16800 0 16800 0
0 0 0 0
S = 8x8
1.0e+04 *
1.6020 0.5940 -1.0080 0 -0.5940 -0.5940 0 0
0.5940 0.5940 0 0 -0.5940 -0.5940 0 0
-1.0080 0 1.5975 -0.1670 -0.4301 0.6452 -0.1594 -0.4781
0 0 -0.1670 2.4021 0.6452 -0.9677 -0.4781 -1.4344
-0.5940 -0.5940 -0.4301 0.6452 2.7041 -0.0512 -1.6800 0
-0.5940 -0.5940 0.6452 -0.9677 -0.0512 1.5617 0 0
0 0 -0.1594 -0.4781 -1.6800 0 1.8394 0.4781
0 0 -0.4781 -1.4344 0 0 0.4781 1.4344The resulting system , however, is singular. In mechanical terms, it contains rigid body motions. In mathematical terms, it has an infinite amount of solutions. To alleviate these rigid body motions, we need to clamp down the mechanical system by introducing boundary conditions which pose enough constraints on the displacements such that rigid body motions are prohibited. This is done for instance by eliminating equations, i.e., rows and columns corresponding to the degrees of freedom where the displacements are known. Solving the reduced system gives a unique solution.
Note that special treatment of the right-hand side is required in cases where the displacements are non-zero. See the section on Truss Analysis for details.
We assign the known boundary conditions and loads.
presc = [1 2 4]; % prescribed degrees of freedom
u(presc) = 0;
f(2*4) = -10000; % a single load at node 4 in the y-direction
free = setdiff(1:dofs, presc); % Free DOFs
u(free) = S(free,free)\f(free) % Solving the systemu = 8x1
0
0
-0.1984
0
0.2467
0.0901
0.4451
-0.9116We can separate the x- and y-components of the displacements into a two column matrix for easier handling in the visualization step below.
U = 4x2
0 0
-0.1984 0
0.2467 0.0901
0.4451 -0.9116We can also compute the resultant of the nodal displacement since it usually is of interest when evaluating requirements. We do this be computing the 2-norm of each row of the matrix (using the vectorized approach of course).
UR = 4x1
0
0.1984
0.2626
1.0145Visualize displacements
figure
hold on
patch('Faces',edges,'Vertices',P,'LineWidth',2)
patch('Faces',edges,'Vertices',P+U*80,'LineWidth',1,'LineStyle',':')
axis equal
axis off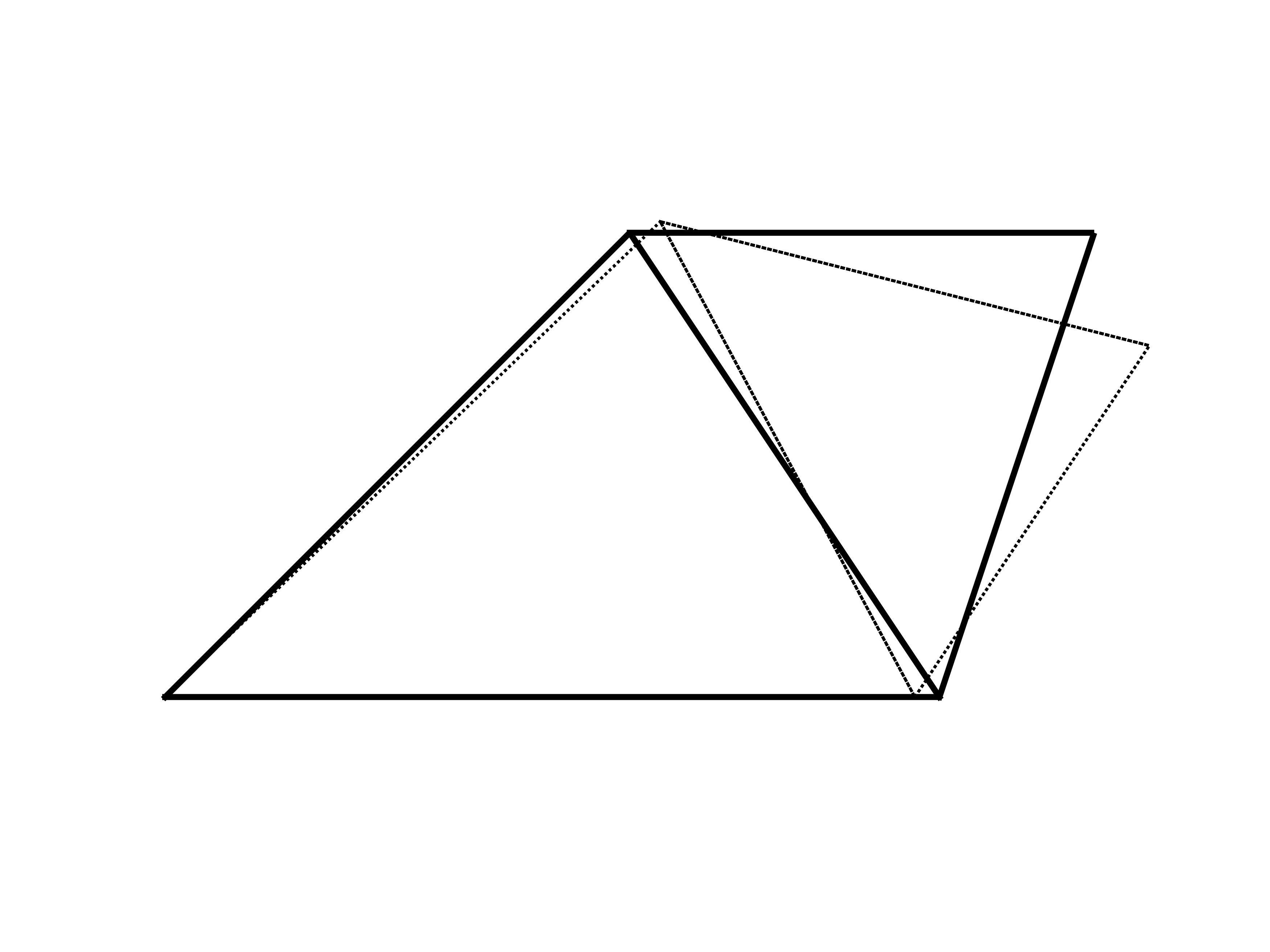
The generated displacement field (dashed line) is scaled up by a factor of 80 since the displacements are otherwise too small to see.
Computing rod quantities
Once the displacements have been computed we can compute the normal forces, resultant forces, deformations, strains and stresses.
React = zeros(dofs,1); % Reaction forces
delta = zeros(nele,1); % Deformation vector
N = delta; % Force vector
epsilon = delta; % Strain vector
sigma = delta; % Stress vector
for iel = 1:nele
inod = edges(iel,:);
ieqs = zeros(1,4); %[0 0 0 0]
ieqs(1:2:end) = inod*2-1;
ieqs(2:2:end) = inod*2;
iu = u(ieqs); % element displacements
p1 = P(inod(1), :);
p2 = P(inod(2), :);
r = p2-p1;
L = norm(r); % length of the bar
er = r/L; % direction, unit vector
c = er(1);
s = er(2);
T = [-c -s c s];
iA = A(iel); % element area
iE = E(iel); % element Young's modulus
k = (iA*iE/L); % element stiffness
idelta = T*iu; % element deformation
iN = k * idelta; % element force
fe = T'*iN; % nodal force
iepsilon = idelta/L; % element strain
isigma = iN/iA; % element stress
React(ieqs) = React(ieqs) + fe; % Add up all reaction forces
N(iel) = iN;
delta(iel) = idelta;
epsilon(iel) = iepsilon;
sigma(iel) = isigma;
end
React = [React(1:2:end), React(2:2:end)] % Reaction forces split into x and y componentsReact = 4x2
1.0e+04 *
0.0000 -0.2000
-0.0000 1.2000
0.0000 -0.0000
-0.0000 -1.0000Once the quantities of interest are computed, we will visualize them on the deformed structure. Since the displacements are typically very small, we will scale up the deformation in order to see a trend.
The quantities will be shown using a color field for a fast overview, but we will also add text boxes to give numerical values for more accurate reading.
scale = 80;
X = P(:,1); Y = P(:,2); Ux = U(:,1); Uy = U(:,2);
Xm = mean(X(edges')+Ux(edges')*scale,1);
Ym = mean(Y(edges')+Uy(edges')*scale,1);
figure; hold on
patch('Faces',edges,'Vertices',P,'EdgeAlpha',0.1)
patch(X(edges')+Ux(edges')*scale,Y(edges')+Uy(edges')*scale,[sigma,sigma]','EdgeColor','flat', 'LineWidth',2)
axis equal
colormap jet; colorbar
text(Xm,Ym,cellstr(num2str(sigma)),'BackgroundColor','w')
title('Member stresses [MPa]')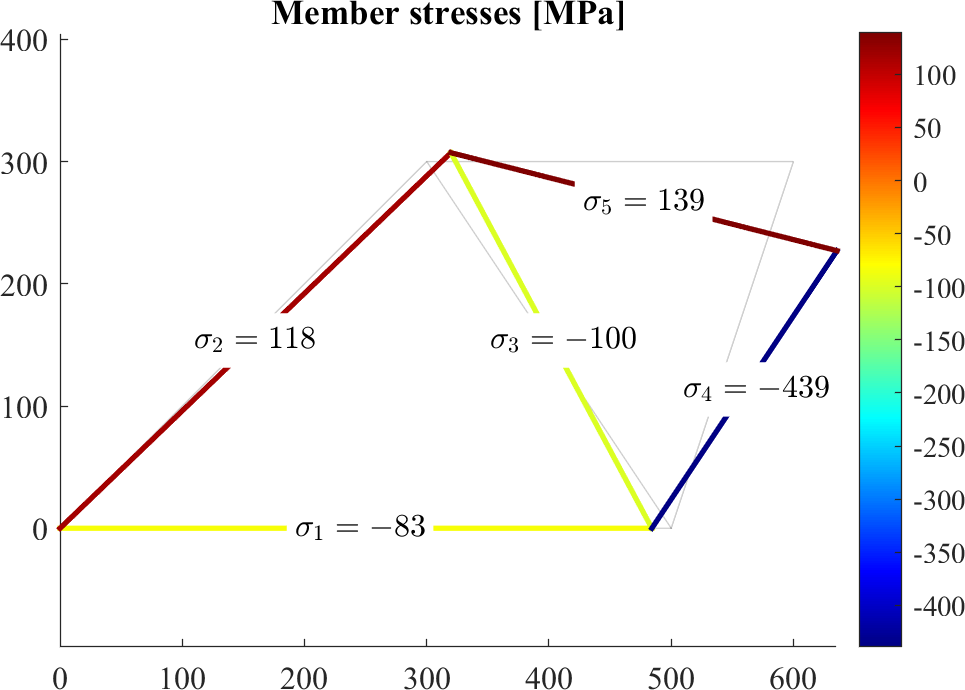
figure; hold on
patch('Faces',edges,'Vertices',P,'EdgeAlpha',0.1)
patch(X(edges')+Ux(edges')*scale,Y(edges')+Uy(edges')*scale,[N,N]','EdgeColor','flat', 'LineWidth',2)
axis equal
colormap jet; colorbar
text(Xm,Ym,cellstr(num2str(N)),'BackgroundColor','w')
title('Member forces [N]')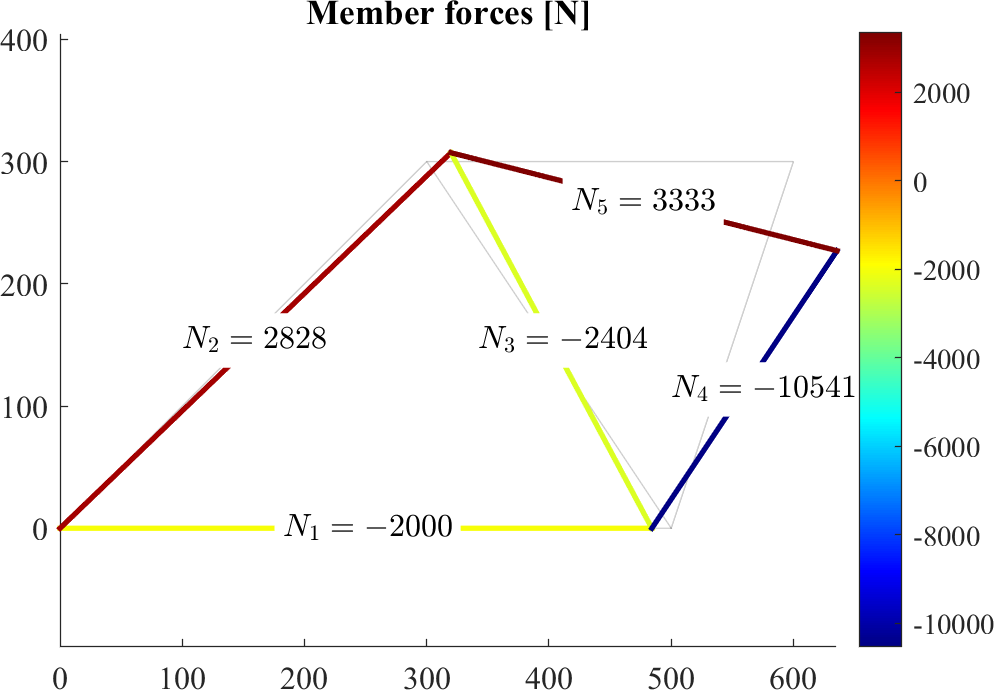
figure; hold on
patch('Faces',edges,'Vertices',P,'EdgeAlpha',0.1)
patch(X(edges')+Ux(edges')*scale,Y(edges')+Uy(edges')*scale,[delta,delta]','EdgeColor','flat', 'LineWidth',2)
axis equal
colormap jet; colorbar
text(Xm,Ym,cellstr(num2str(delta)),'BackgroundColor','w')
title('Member deformations [mm]')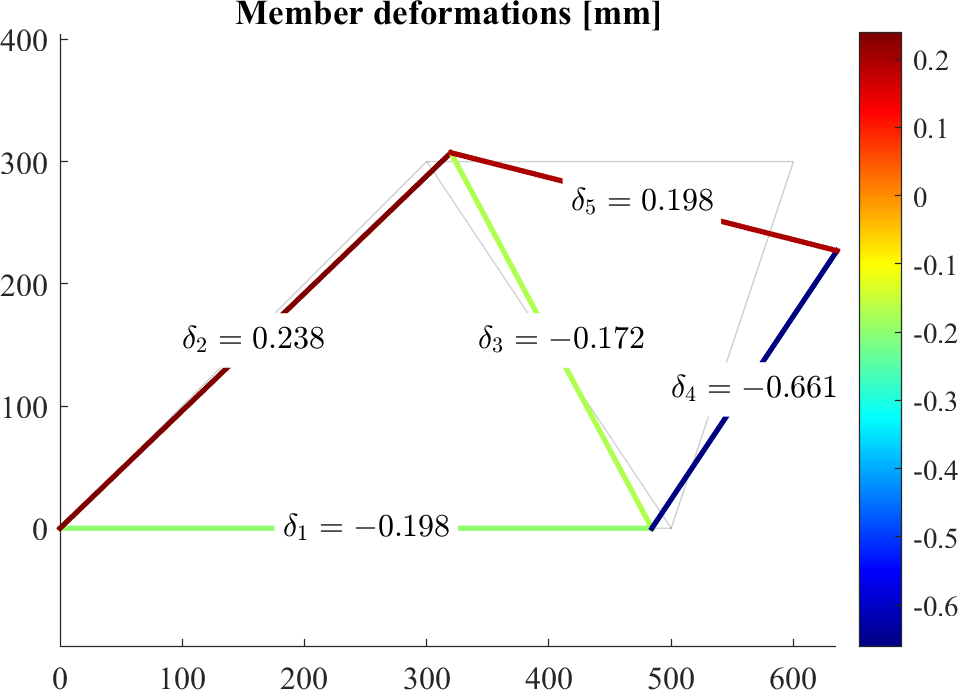
figure; hold on
patch('Faces',edges,'Vertices',P,'EdgeAlpha',0.1)
patch(X(edges')+Ux(edges')*scale,Y(edges')+Uy(edges')*scale,[epsilon,epsilon]','EdgeColor','flat', 'LineWidth',2)
axis equal
colormap jet; colorbar
text(Xm,Ym,cellstr(num2str(epsilon)),'BackgroundColor','w')
title('Member strains [mm/mm]')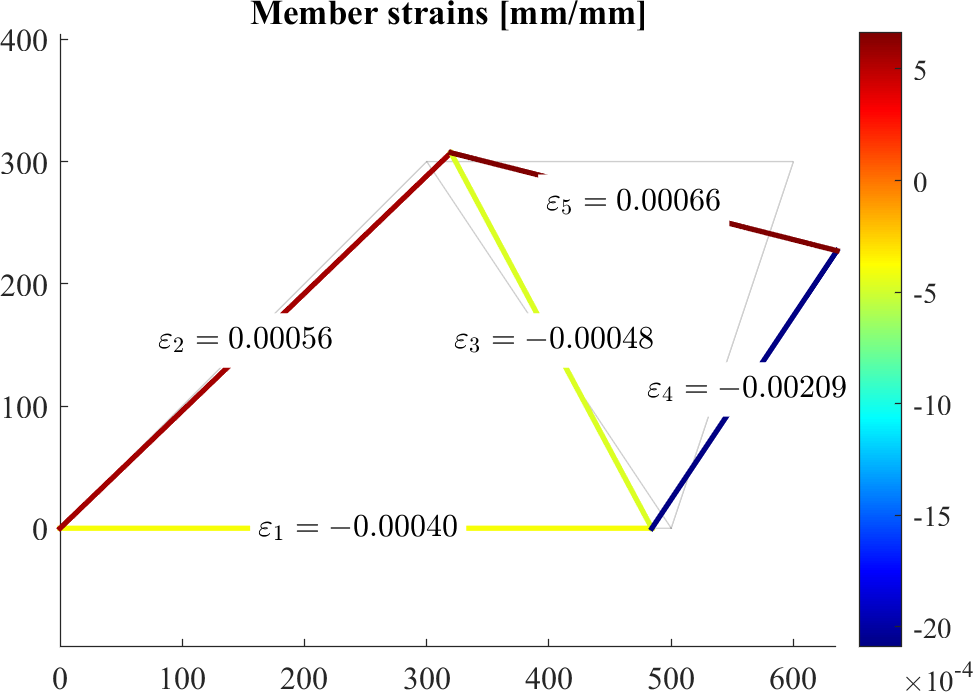
Here, in addition for nodal forces, we also have nodes with prescribed displacements which are non-zero. This is the same as deforming a spring to a certain length, it will correspond to a force, but we control the displacement instead.
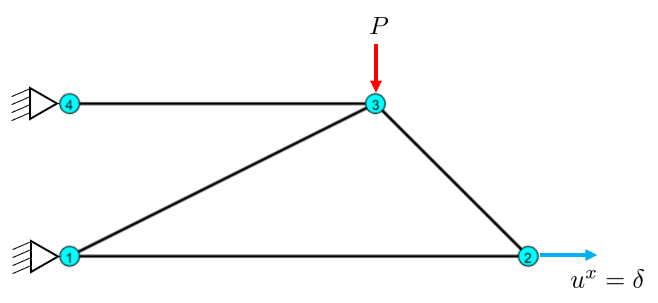
mm. kN.
clear
P = [0 0
6 0
4 2
0 2]*100; % mm
nnod = size(P,1);
edges = [1 2
3 4
1 3
3 2];Initiate variables
nele = size(edges,1);
nnod = size(P,1);
dofs = nnod*2; %number of degrees of freedom
S = zeros(dofs, dofs);
f = zeros(dofs,1);
u = f;
Sprim = [1 0 -1 0
0 0 0 0
-1 0 1 0
0 0 0 0];
Ltot = 0; % Total length of the structure.Visualize the structure
figure; hold on
patch('Faces',edges,'Vertices',P,'LineWidth',2, 'HandleVisibility','off')
dx = max(P(:,1))-min(P(:,1));
dy = max(P(:,2))-min(P(:,2));
plot(P(:,1),P(:,2),'ok','MarkerFaceColor','k','MarkerSize',14, 'HandleVisibility','off')
text(P(:,1)-0.01*dx,P(:,2),cellstr(num2str([1:nnod]')),'Color','w', 'HandleVisibility','off');
axis equal
axis off
for i=1:nele
inod = edges(i,:);
xm = mean(P(inod,1));
ym = mean(P(inod,2));
text(xm,ym,num2str(i),'backgroundColor','y')
endUser defined parameters
E = 210000*ones(nele,1); % Young's modulus
A = 4*6*ones(nele,1); % Cross sectional area
presc = [1 2 3 7 8]; % prescribed degrees of freedom
u(presc) = [0, 0, 2, 0, 0]; %mm
f(3*2) = -10000;free = setdiff(1:dofs, presc); % Free DOFsVisualize the Load case
To visually verify load case and boundary conditions
px = presc(mod(presc,2)==1);
xinds = (px+1)/2;
py = presc(mod(presc,2)==0);
yinds = py/2;
Fx = f(1:2:end); Fy = f(2:2:end);
dd = sqrt(dx^2+dy^2);
quiver(P(:,1)+sign(Fx)*dd*0.03,P(:,2),Fx,zeros(nnod,1),0.08,'Color','r','LineWidth',2,'DisplayName','f_x')
quiver(P(:,1),P(:,2)+sign(Fy)*dd*0.03,zeros(nnod,1),Fy,0.08,'Color','b','LineWidth',2,'DisplayName','f_y')
plot(P(xinds,1),P(xinds,2),'sk','MarkerFaceColor','r','MarkerSize',25,'DisplayName','u_x');
plot(P(yinds,1),P(yinds,2),'dk','MarkerFaceColor','b','MarkerSize',14,'DisplayName','u_y');
text(P(:,1)-0.01*dx,P(:,2),cellstr(num2str([1:nnod]')),'Color','w','HandleVisibility','off');
legend show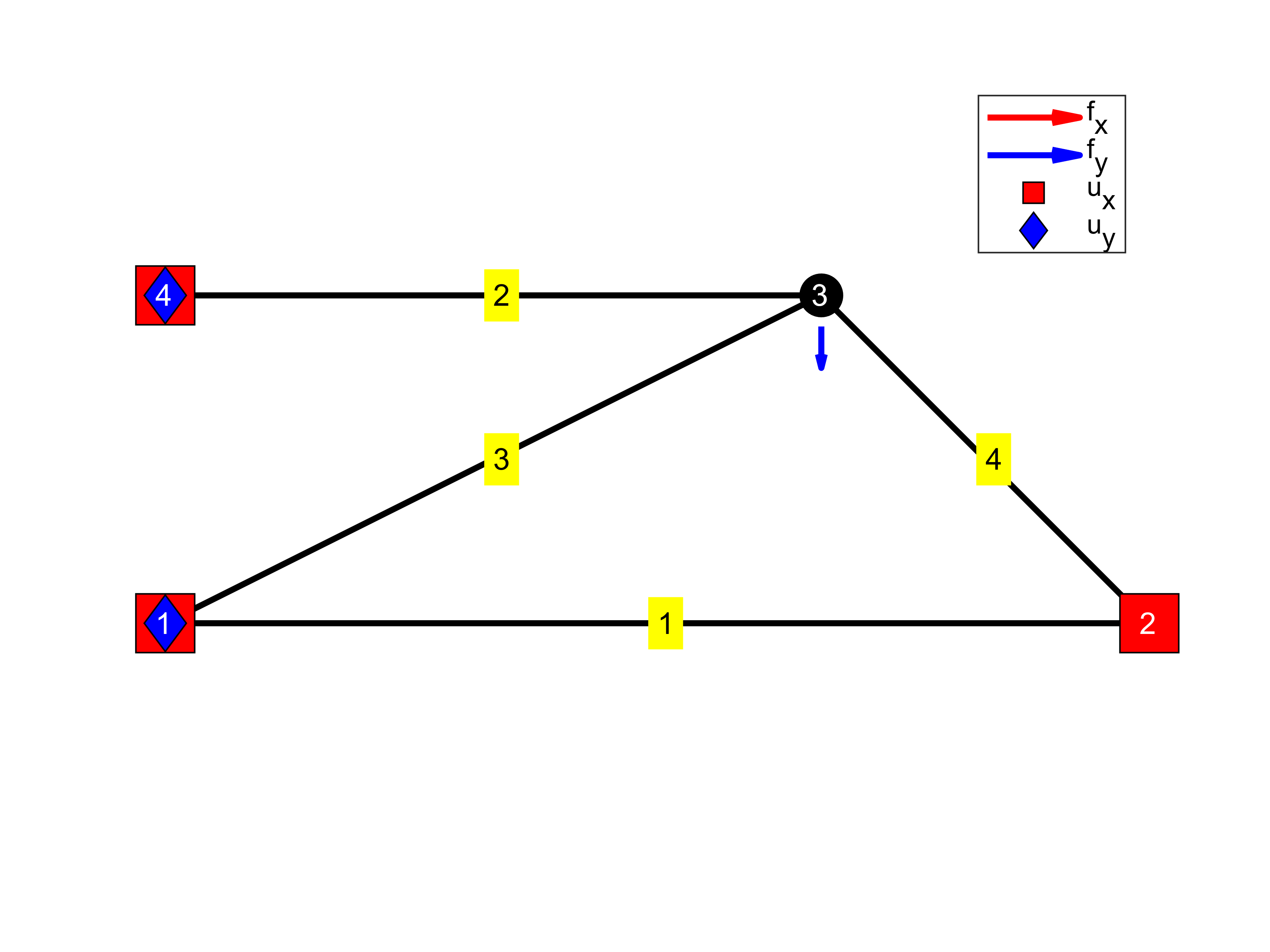
Computing the stiffness matrix
for iel = 1:nele
inod = edges(iel,:);
ieqs = zeros(1,4); %[0 0 0 0]
ieqs(1:2:end) = inod*2-1;
ieqs(2:2:end) = inod*2;
p1 = P(inod(1), :);
p2 = P(inod(2), :);
r = p2-p1;
L = norm(r); % length of the bar
Ltot = Ltot + L;
er = r/L; % direction, unit vector
c = er(1);
s = er(2);
R = [c -s
s c];
% Transformation matrix
LT = [R, zeros(2);
zeros(2), R];
% Element stiffness matrix
iA = A(iel); % element area
iE = E(iel); % element Young's modulus
k = (iA*iE/L); % element stiffness
Se = k * LT*Sprim*LT';
S(ieqs,ieqs) = S(ieqs,ieqs) + Se ;
endNow we deal with the prescribed displacements.
fr = 8x1
1.0e+04 *
-1.6800
0
3.4619
-1.7819
-1.7819
1.7819
0
0f = 8x1
1.0e+04 *
1.6800
0
-3.4619
1.7819
1.7819
-2.7819
0
0u(free) = S(free,free)\f(free);
U = [u(1:2:end), u(2:2:end)]U = 4x2
0 0
2.0000 -7.1985
1.5873 -7.6112
0 0UR = sum(U.^2,2).^0.5 % Resultant displacementUR = 4x1
0
7.4712
7.7750
0Visualize the displacements
scale = 5;
figure
hold on
patch('Faces',edges,'Vertices',P,'LineWidth',2)
patch('Faces',edges,'Vertices',P+U*scale,'LineWidth',1,'LineStyle',':')
axis equal
axis off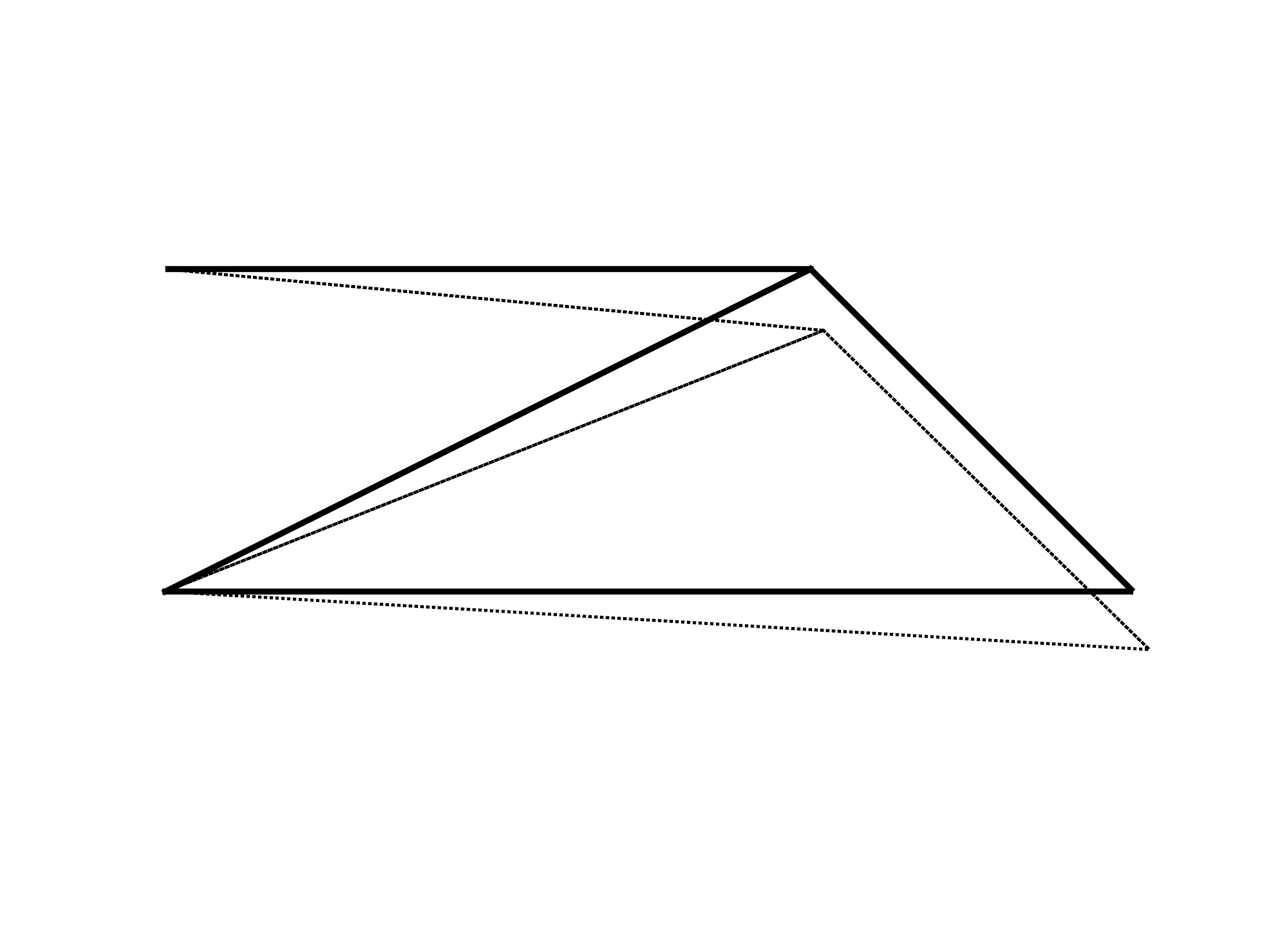
Computing rod quantities
React = zeros(dofs,1);
delta = zeros(nele,1);
N = delta; epsilon = delta; sigma = delta;
for iel = 1:nele
inod = edges(iel,:);
ieqs = zeros(1,4); %[0 0 0 0]
ieqs(1:2:end) = inod*2-1;
ieqs(2:2:end) = inod*2;
iu = u(ieqs);
p1 = P(inod(1), :);
p2 = P(inod(2), :);
r = p2-p1;
L = norm(r); % length of the bar
er = r/L; % direction, unit vector
c = er(1);
s = er(2);
R = [c -s
s c];
% Transformation matrix
LT = [R, zeros(2);
zeros(2), R];
T = [-c -s c s];
iA = A(iel); % element area
iE = E(iel); % element Young's modulus
k = (iA*iE/L); % element stiffness
idelta = T*iu;
iN = k * idelta;
fe = T'*iN;
iepsilon = idelta/L;
isigma = iN/iA;
React(ieqs) = React(ieqs) + fe;
N(iel) = iN;
delta(iel) = idelta;
epsilon(iel) = iepsilon;
sigma(iel) = isigma;
endThe reaction forces in each node.
React = [React(1:2:end), React(2:2:end)]React = 4x2
1.0e+04 *
0.3200 1.0000
1.6800 0.0000
0.0000 -1.0000
-2.0000 0Visualize color fields
X = P(:,1); Y = P(:,2); Ux = U(:,1); Uy = U(:,2);
Xm = mean(X(edges')+Ux(edges')*scale,1);
Ym = mean(Y(edges')+Uy(edges')*scale,1);
figure; hold on
patch('Faces',edges,'Vertices',P,'EdgeAlpha',0.1)
patch(X(edges')+Ux(edges')*scale,Y(edges')+Uy(edges')*scale,[sigma,sigma]','EdgeColor','flat', 'LineWidth',2)
axis equal
colormap jet; colorbar
for iel=1:nele
text(Xm(iel),Ym(iel),sprintf('$\\sigma_{%d}=%0.0f$',iel,sigma(iel)),'BackgroundColor','w','Interpreter','latex')
end
title('Member stresses [MPa]')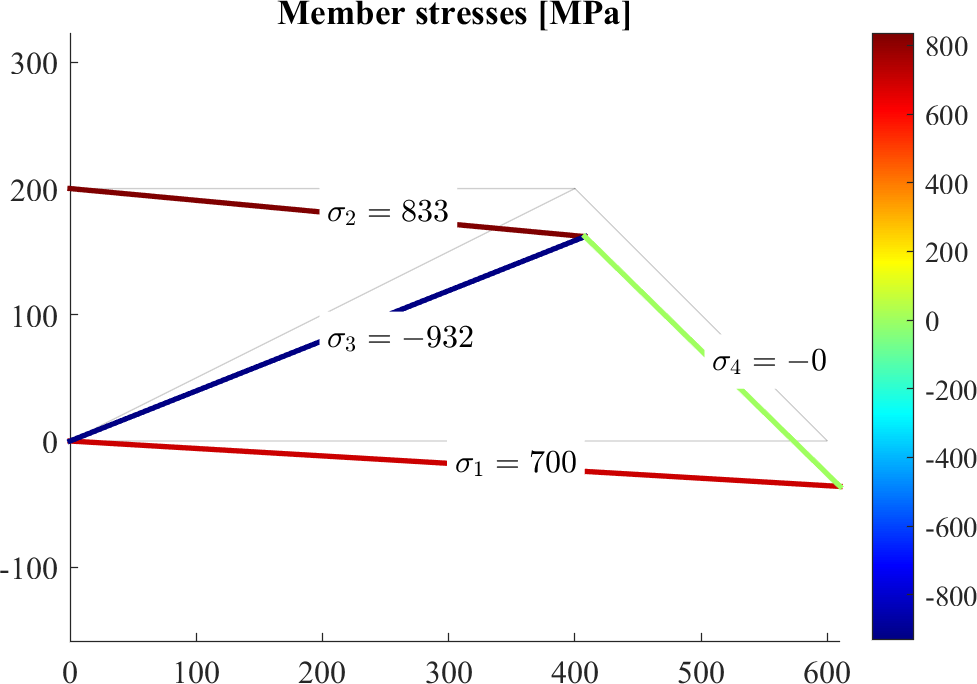
figure; hold on
patch('Faces',edges,'Vertices',P,'EdgeAlpha',0.1)
patch(X(edges')+Ux(edges')*scale,Y(edges')+Uy(edges')*scale,[N,N]','EdgeColor','flat', 'LineWidth',2)
axis equal
colormap jet; colorbar
for iel=1:nele
text(Xm(iel),Ym(iel),sprintf('$N_{%d}=%0.0f$',iel,N(iel)),'BackgroundColor','w','Interpreter','latex')
end
title('Member forces [N]')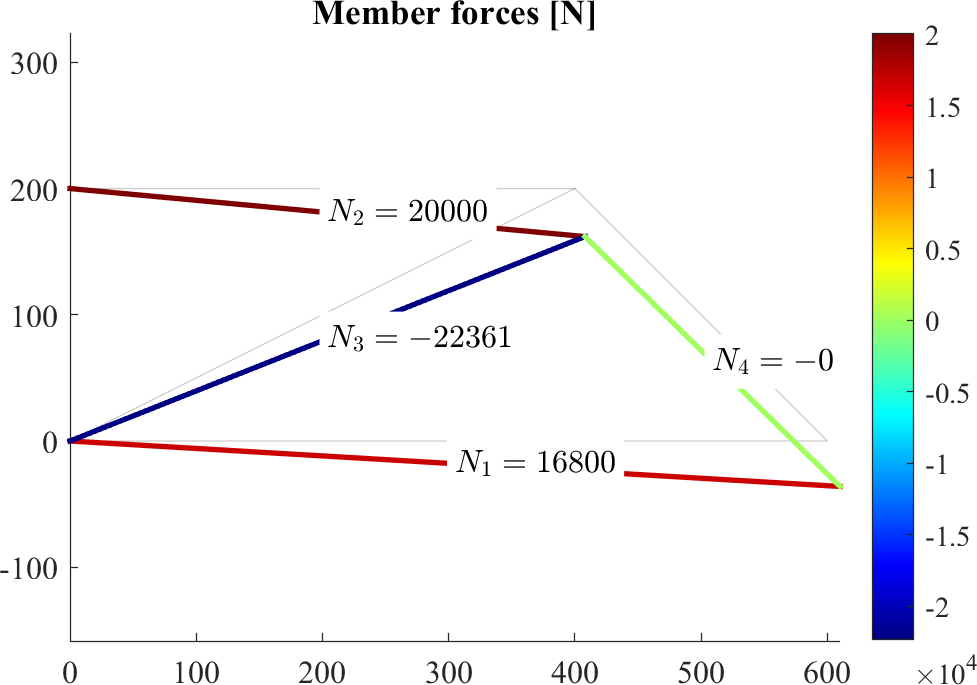
figure; hold on
patch('Faces',edges,'Vertices',P,'EdgeAlpha',0.1)
patch(X(edges')+Ux(edges')*scale,Y(edges')+Uy(edges')*scale,[delta,delta]','EdgeColor','flat', 'LineWidth',2)
axis equal
colormap jet; colorbar
for iel=1:nele
text(Xm(iel),Ym(iel),sprintf('$\\delta_{%d}=%0.3f$',iel,delta(iel)),'BackgroundColor','w','Interpreter','latex')
end
title('Member deformations [mm]')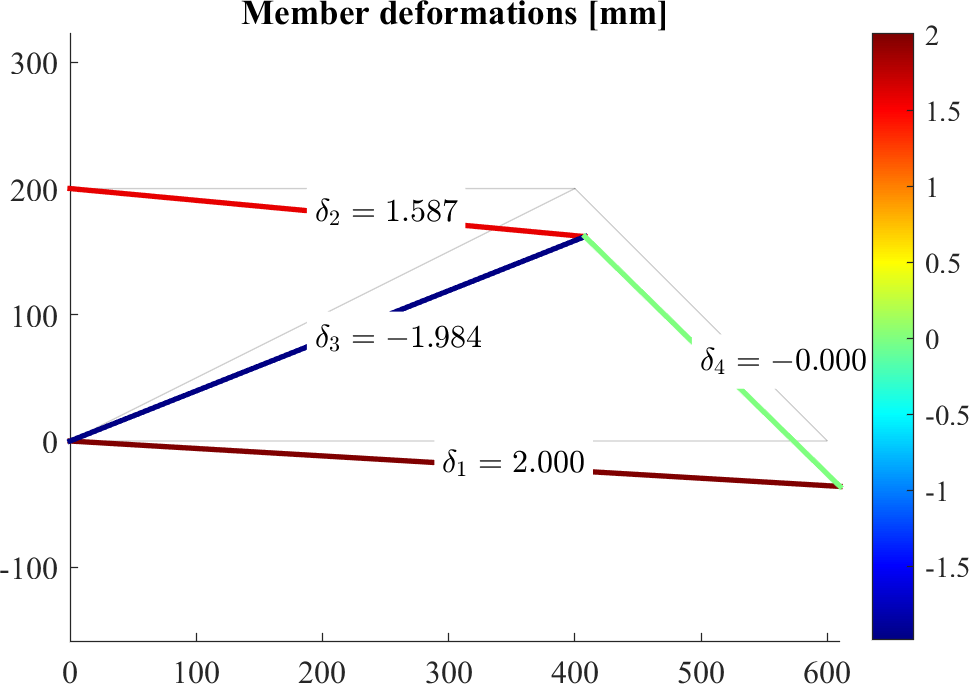
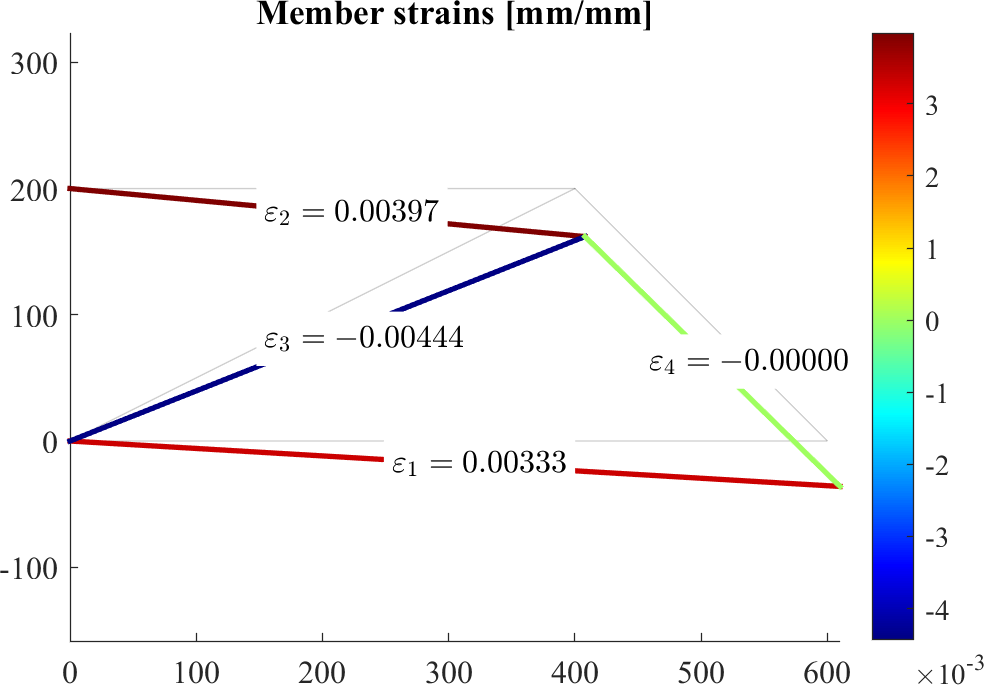
figure; hold on
patch('Faces',edges,'Vertices',P,'EdgeAlpha',0.1)
patch(X(edges')+Ux(edges')*scale,Y(edges')+Uy(edges')*scale,[epsilon,epsilon]','EdgeColor','flat', 'LineWidth',2)
axis equal
colormap jet; colorbar
for iel=1:nele
text(Xm(iel),Ym(iel),sprintf('$\\varepsilon_{%d}=%0.5f$',iel,epsilon(iel)),'BackgroundColor','w','Interpreter','latex')
end
title('Member strains [mm/mm]')